Thread Value Layouts in CuTe

28 Jun, 2025

Thread Value Layout is a concept commonly used in CuTeDSL kernels. In this blogpost we aim to give a brief intuitive understanding of the concepts. We will provide visuals as this deepens understanding of the underlying concept and provides intuitive way to understand it.

Problem description

Following situation:

We have an array layed out in memory. Layout in memory is linear and we assume that each element is next to the preceding and proceeding element. We want to perform the following task: Assign $N$ values in memory to $N_{threads}$ threads in a way that we can draw.

Let's consider the following example:

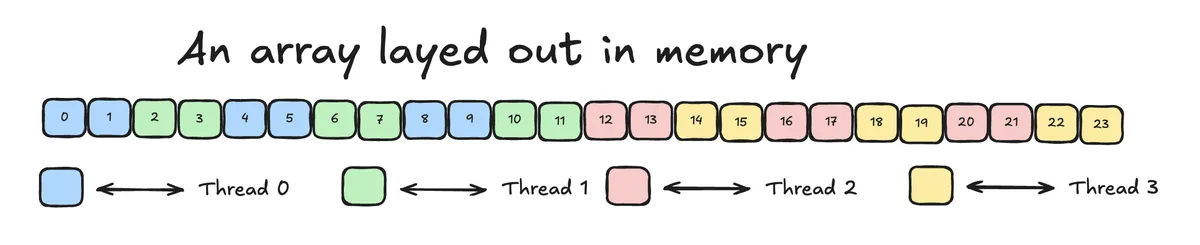
It is not immediately obvious how we would could come up with the appropriate indexing that archives this assignment. Fortunately CuTe layouts provide a convenient way to make such an assignment.

Value Layout

We start with the value layout for one Thread. Let's consider the blue elements above. We could arrange them as follows in a matrix:

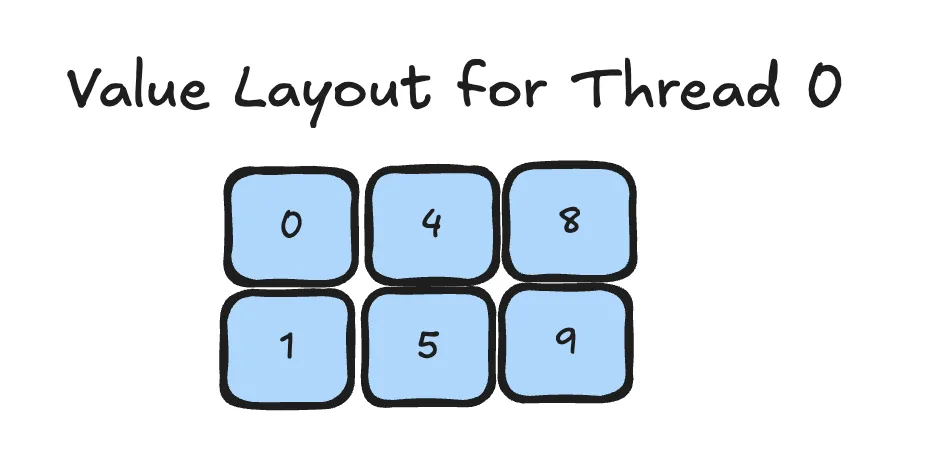
Let us think how we could obtain such an arangment using CuTe Layouts:

• We have 2 rows and 3 columns
• When we go down in mode 0, i.e. the row, the value increases by 1
• When we go to the right in mode 1, i.e. the column, the value increases by 4

Thus the layout can be written down as $(2,3):(1,4)$.

You can verify yourself this is indeed the "rule" we may use to obtain the value layout for all 4 threads.

Thread layout

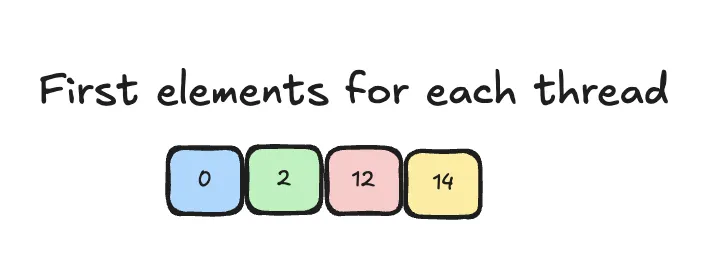
We have 4 threads to assign. So the thread layout should have a size of 4.

Above we have already fully described the values assigned to each thread. So we may drop everything but the first index of each thread to describe the threads. All the other values can be obtained from the value layout.

Here is a picture to help understanding:

To obtain the corresponding layout lets rearrange that into a matrix:

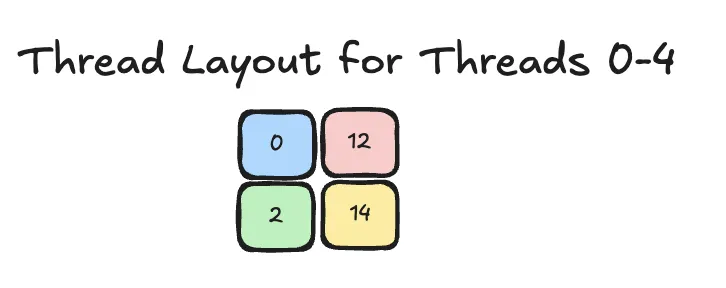
• We see that the matrix has shape 2 by 2
• We see that to go down we need to increase by 2
• We see that to go right we need to increase by 12

That gives us the thread layout $(2,2):(2,12)$.

Thread Value Layout

The full Thread Value Layout looks as follows:

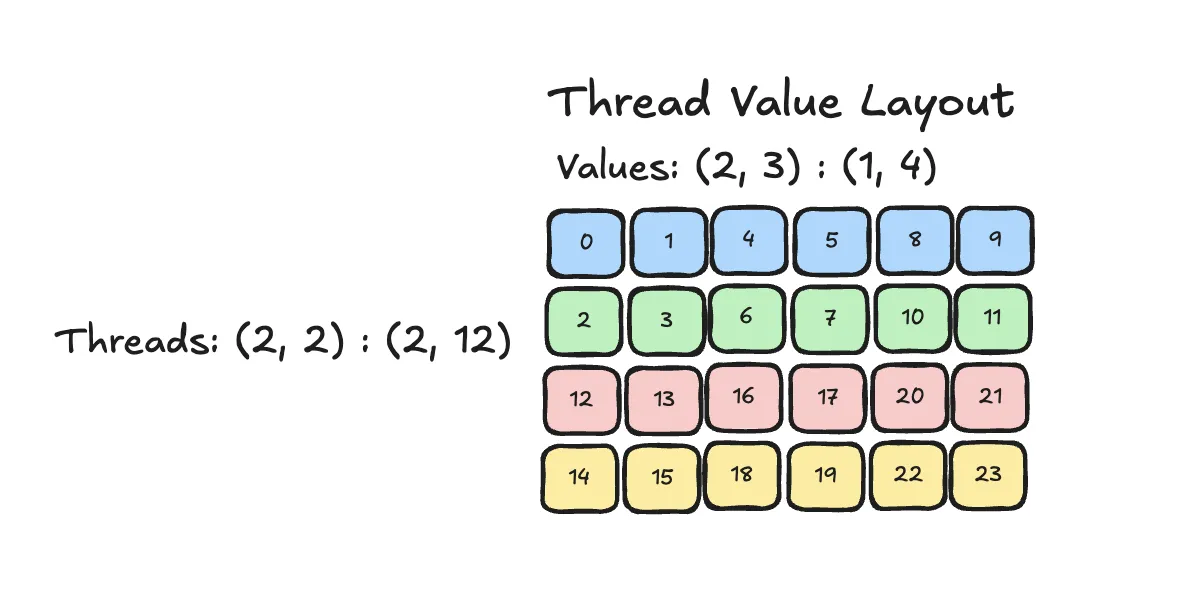
As derived above we can obtain each Thread by the Thread Layout and than the corresponding values can be obtained with the Value Layout.

The full layout can be written as $((2,2),(2,3)):((2,12),(1,4))$. It is nice to see that this seemingly complex expression has actually pretty simple meaning. The associated layout function will map (thread_index, value_index) -> 1D coordinate of array.

CuTeDSL implementation

We can verify our ideas above as follows in CuTeDSL

import torch

import cutlass.cute as cute
from cutlass.cute.runtime import from_dlpack


@cute.kernel
def visualize_tv_layout_kernel(mA: cute.Tensor, tv_layout: cute.Layout):
    tidx, _, _ = cute.arch.thread_idx()
    # Compose mA with TV Layout
    composed = cute.composition(mA, tv_layout)
    cute.printf("TIDX: {}", tidx)
    cute.printf("DATA: {}", composed[(tidx, None)])


@cute.jit
def visualize_tv_layout(
    mA: cute.Tensor,
):
    # mA Layout: (24, 1) : (1, 0)
    tv_layout = cute.make_layout(shape=((2, 2), (2, 3)), stride=((2, 12), (1, 4)))
    print(f"TV Layout: {tv_layout}")

    # Launch the kernel asynchronously
    # Async token(s) can also be specified as dependencies
    visualize_tv_layout_kernel(mA, tv_layout).launch(
        grid=[1, 1, 1],
        block=[cute.size(tv_layout, mode=[0]), 1, 1],
    )


if __name__ == "__main__":
    M, N = 24, 1
    a = torch.arange(M * N, device="cuda", dtype=torch.int32).reshape(M, N)
    a_ = from_dlpack(a, assumed_align=16)

    visualize_tv_layout(a_)

This will print out

TV Layout: ((2,2),(2,3)):((2,12),(1,4))
TIDX: 0
DATA: raw_ptr(0x00007fc4f5e00000: i32, gmem, align<8>) o ((2,3)):((1,4)) = 
  ( 0, 1, 4, 5, 8, 9 )
TIDX: 1
DATA: raw_ptr(0x00007fc4f5e00008: i32, gmem, align<8>) o ((2,3)):((1,4)) = 
  ( 2, 3, 6, 7, 10, 11 )
TIDX: 2
DATA: raw_ptr(0x00007fc4f5e00030: i32, gmem, align<8>) o ((2,3)):((1,4)) = 
  ( 12, 13, 16, 17, 20, 21 )
TIDX: 3
DATA: raw_ptr(0x00007fc4f5e00038: i32, gmem, align<8>) o ((2,3)):((1,4)) = 
  ( 14, 15, 18, 19, 22, 23 )

Which confirms our thought process above.

Our tensor is equipped with a Layout of (24, 1) : (1, 1). Note that in principle we could also use a different layout. By composing it with the TV Layout we obtain a map from (thread_idx, value_idx) -> coordinate to index into data -> underlying data.

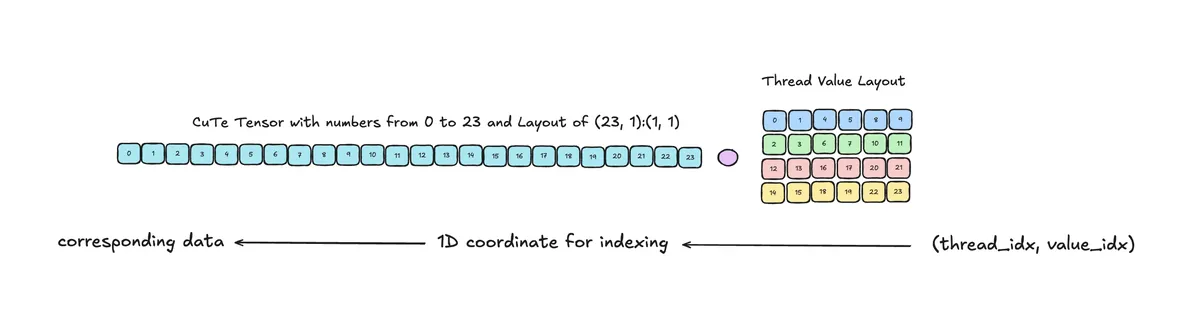
Inside the kernel we first compose and than slice (into the corresponding thread index via (tidx, None) where None is similar to : in numpy). This is called partioning.

Conclusion

I hope this blogpost made the concept of Thread Value Layout which seems hard to understand at first easy accessible. I think to understand CuTeDSL deeper it is necessary to understand the fundamentals used often deeply.

If you want to discuss CuTe or other GPU related topic you may contact me via Linkedin.