Programming tensor cores in Mojo
The mma PTX instruction is essential to understand in depth to being able to program NVIDIA GPUs.
In the past I did a blogpost on the mma instruction which you might to take a look at in order to understand the terminology of this blogpost.
Using the mma Mojo API
fn mma_sync_16x8x16_bf16_fp32():
a = SIMD[DType.bfloat16, 8](1.0)
b = SIMD[DType.bfloat16, 4](1.0)
c = SIMD[DType.float32, 4](0.0)
d = SIMD[DType.float32, 4](0.0)
mma(d, a, b, c)
_printf["thread %d : %g %g %g %g\n"](
thread_idx.x,
d[0].cast[DType.float64](),
d[1].cast[DType.float64](),
d[2].cast[DType.float64](),
d[3].cast[DType.float64](),
)
This kernel will simply perform a warp level MMA operation, i.e. D = A * B + C.
A and B are in bfloat16 format while C and D are in float32 type. This is a pretty common setup in AI applications where we oftentimes perform multiplication of weights and activations in bfloat16 for efficency.
The printf is simply to visualize that everything works as expected and will print out
thread 0 : 16 16 16 16
thread 1 : 16 16 16 16
thread 2 : 16 16 16 16
thread 3 : 16 16 16 16
thread 4 : 16 16 16 16
thread 5 : 16 16 16 16
thread 6 : 16 16 16 16
thread 7 : 16 16 16 16
thread 8 : 16 16 16 16
thread 9 : 16 16 16 16
thread 10 : 16 16 16 16
thread 11 : 16 16 16 16
thread 12 : 16 16 16 16
thread 13 : 16 16 16 16
thread 14 : 16 16 16 16
thread 15 : 16 16 16 16
thread 16 : 16 16 16 16
thread 17 : 16 16 16 16
thread 18 : 16 16 16 16
thread 19 : 16 16 16 16
thread 20 : 16 16 16 16
thread 21 : 16 16 16 16
thread 22 : 16 16 16 16
thread 23 : 16 16 16 16
thread 24 : 16 16 16 16
thread 25 : 16 16 16 16
thread 26 : 16 16 16 16
thread 27 : 16 16 16 16
thread 28 : 16 16 16 16
thread 29 : 16 16 16 16
thread 30 : 16 16 16 16
thread 31 : 16 16 16 16
Which makes sense because the contracted dimension is K = 16.
How to implement custom mma instruction
As of today the Mojo std doesn't support the mma operation where M = 16, N = 8, K = 16 and all the matrices are in float16.
We could either write directly in inline assembly the PTX instruction or we can use the corresponding llvm intrinsic. Here I will choose llvm intrinsic.
We can take a look at the llvm repo to understand the format we need to implement:
// CHECK-LABEL: @nvvm_mma_m16n8k16_f16_f16
llvm.func @nvvm_mma_m16n8k16_f16_f16(%a0 : vector<2xf16>, %a1 : vector<2xf16>,
%a2 : vector<2xf16>, %a3 : vector<2xf16>,
%b0 : vector<2xf16>, %b1 : vector<2xf16>,
%c0 : vector<2xf16>, %c1 : vector<2xf16>) -> !llvm.struct<(vector<2xf16>, vector<2xf16>)> {
// CHECK: call { <2 x half>, <2 x half> } @llvm.nvvm.mma.m16n8k16.row.col.f16.f16
%0 = nvvm.mma.sync A[ %a0, %a1, %a2, %a3 ] B[ %b0, %b1 ] C[ %c0, %c1 ]
{layoutA = #nvvm.mma_layout<row>, layoutB = #nvvm.mma_layout<col>, shape = #nvvm.shape<m = 16, n = 8, k = 16>}
: (vector<2xf16>, vector<2xf16>, vector<2xf16>) -> !llvm.struct<(vector<2xf16>, vector<2xf16>)>
llvm.return %0 : !llvm.struct<(vector<2xf16>, vector<2xf16>)>
}
We see from this intrinsics that the instruction expects 4 2 x float16 registers for a, 2 2 x float16 registers for b, 2 2 x float16 registers for c and returns 2 2 x float16 register values.
We can implement this using Mojos SIMD type as follows:
fn mma_wrapper(mut d: SIMD, a: SIMD, b: SIMD, c: SIMD):
var sa = a.split()
var ssa = sa[0].split()
var ssa1 = sa[1].split()
var sb = b.split()
var sc = c.split()
var r = llvm_intrinsic[
"llvm.nvvm.mma.m16n8k16.row.col.f16.f16",
_RegisterPackType[SIMD[DType.float16, 2], SIMD[DType.float16, 2]],
](ssa[0], ssa[1], ssa1[0], ssa1[1], sb[0], sb[1], sc[0], sc[1])
d = rebind[__type_of(d)](r[0].join(r[1]))
fn mma_sync_16x8x16_fp16_fp16():
a = SIMD[DType.float16, 8](1.0)
b = SIMD[DType.float16, 4](1.0)
c = SIMD[DType.float16, 4](0.0)
d = SIMD[DType.float16, 4](0.0)
mma_wrapper(d, a, b, c)
_printf["thread %d : %g %g %g %g\n"](
thread_idx.x,
d[0].cast[DType.float64](),
d[1].cast[DType.float64](),
d[2].cast[DType.float64](),
d[3].cast[DType.float64](),
)
Printing this out will confirm that this instruction is correct and we can check emit the LLVM IR code to confirm:
%5 = call { <2 x half>, <2 x half> } @llvm.nvvm.mma.m16n8k16.row.col.f16.f16(<2 x half> %2, <2 x half> splat (half 0xH3C00), <2 x half> %3, <2 x half> splat (half 0xH3C00), <2 x half> %3, <2 x half> splat (half 0xH3C00), <2 x half> %4, <2 x half> zeroinitializer)
Indeed our instruction is called as expected.
Efficent transfer to registers.
Tensor Cores expect a specific layout for the inputs.
We can see how the layouts should look like for our instruction in the PTX docs:
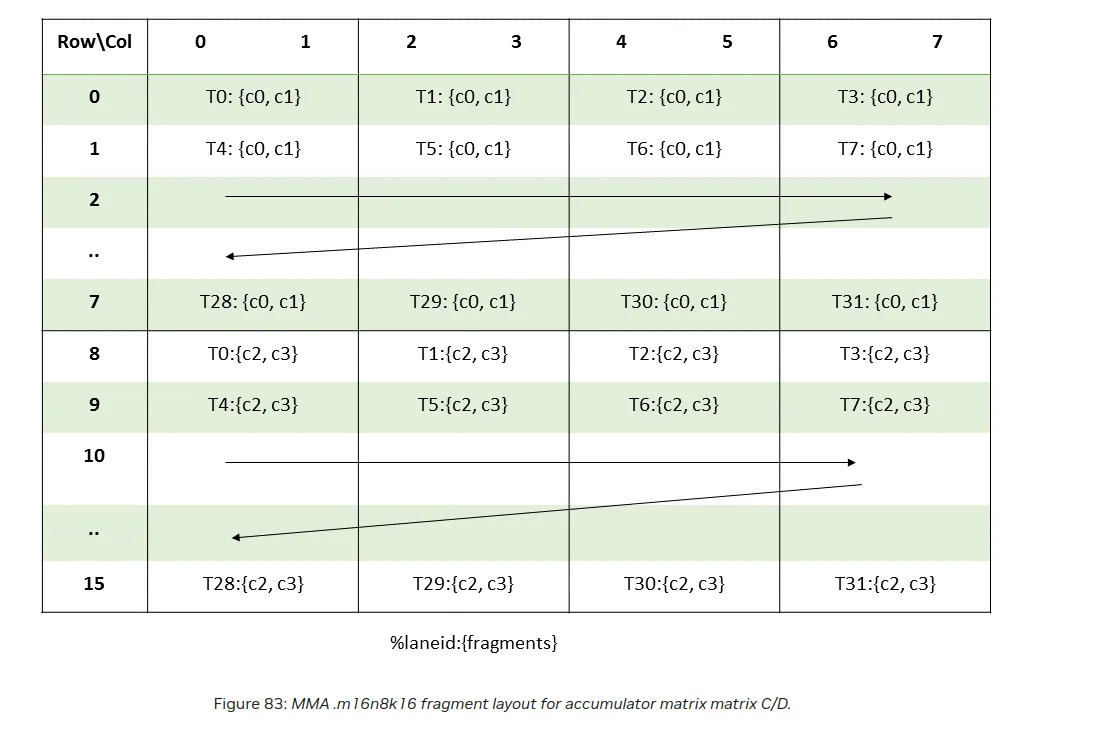
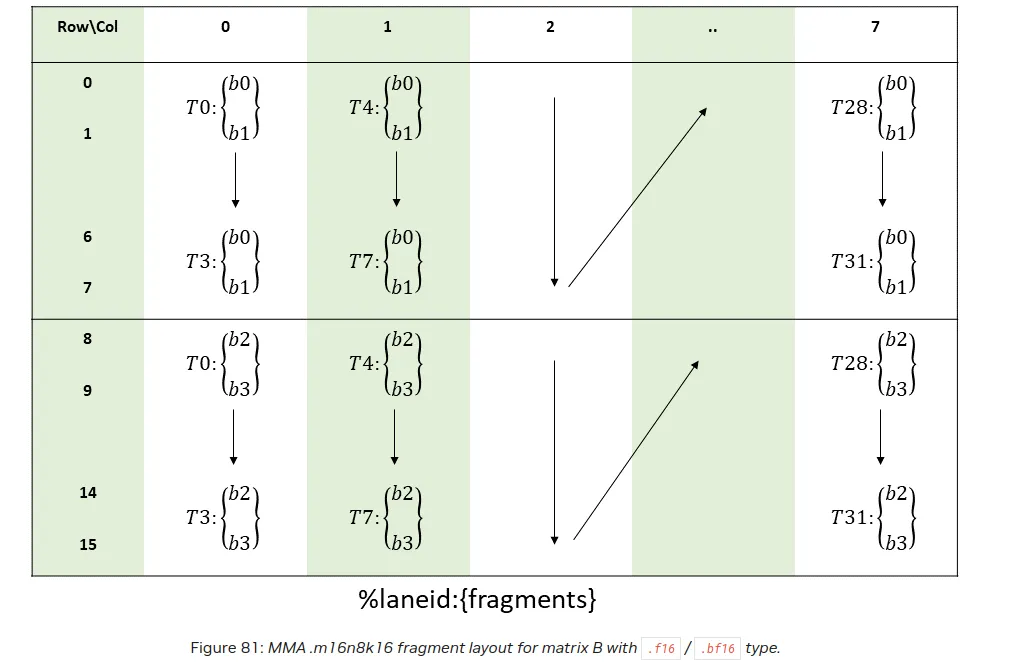
Mojo offers a convenient wrapper that loads a given matrix in this form in the registers, load_matrix_a and load_matrix_b. Please take a look at the implementation. It can be also very useful for CUDA programmers because the mma instruction is only available via PTX in CUDA and figuring out the layout mapping can be a bit tricky.
We can verify the layout is indeed loaded by the Mojo api as follows.
fn mma_with_load[M: Int, N:Int, K:Int](A: UnsafePointer[BFloat16], B: UnsafePointer[BFloat16]):
a = load_matrix_a[M, N, K](A, 0, 0, K)
b = load_matrix_b[M, N, K](B, 0, 0, N)
c = SIMD[DType.float32, 4](0.0)
d = SIMD[DType.float32, 4](0.0)
mma(d, a, b, c)
_printf["thread %d : a: %g, %g, %g, %g %g, %g, %g, %g, b: %g, %g, %g, %g, d: %g %g %g %g\n"](
thread_idx.x,
a[0].cast[DType.float64](),
a[1].cast[DType.float64](),
a[2].cast[DType.float64](),
a[3].cast[DType.float64](),
a[4].cast[DType.float64](),
a[5].cast[DType.float64](),
a[6].cast[DType.float64](),
a[7].cast[DType.float64](),
b[0].cast[DType.float64](),
b[1].cast[DType.float64](),
b[2].cast[DType.float64](),
b[3].cast[DType.float64](),
d[0].cast[DType.float64](),
d[1].cast[DType.float64](),
d[2].cast[DType.float64](),
d[3].cast[DType.float64](),
)
Here we print out the register values for each thread. On the host we initialize for example the matrix A as follows:
A = ctx.enqueue_create_buffer[DType.bfloat16](M * K)
with A.map_to_host() as A_host:
for i in range(M):
for j in range(K):
A_host[i * K + j] = i * K + j
A_ptr = A.unsafe_ptr()
We than can observe
thread 0 : a: 0, 1, 128, 129 8, 9, 136, 137
We can see that is exactly how our layout works:
a0, a1 = 0, 1, a2, a3 = 128, 129, a4, a5 = 8, 9, a6, a7 = 136, 137.
To get a deeper understanding please use the script I provide to play around with it and get a better understanding.
For store we have a similar layout
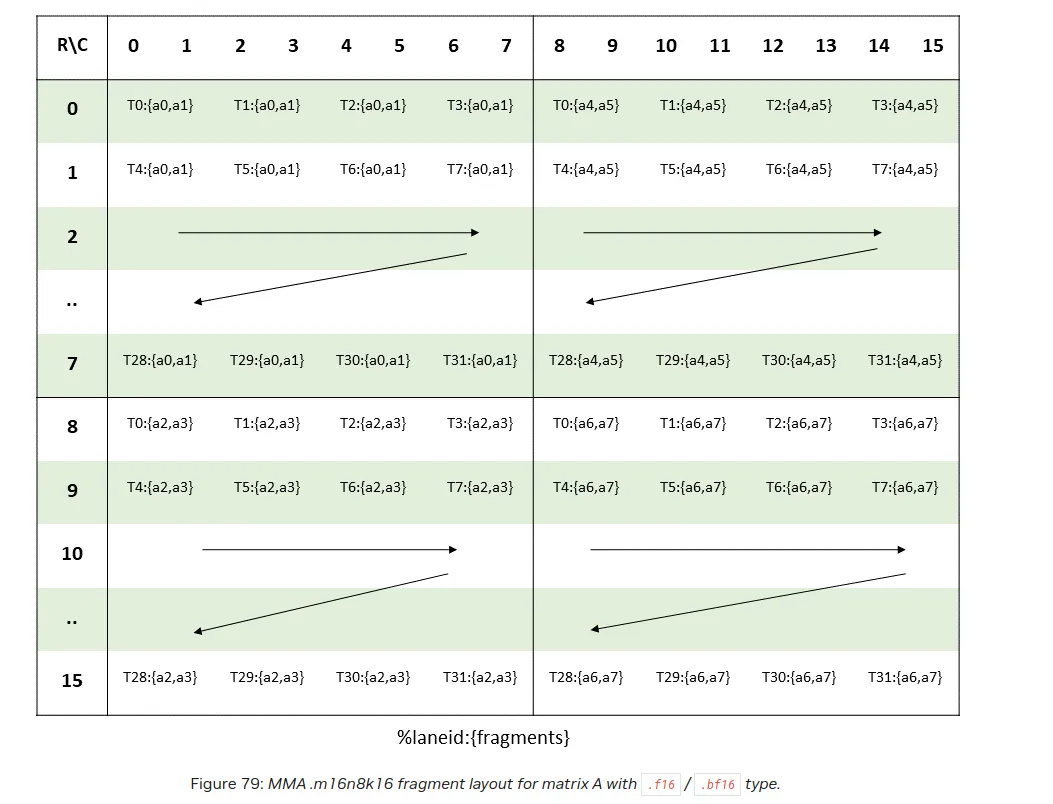
In Mojo we can call store_matrix_d API.
A full example to load matrices correctly into registers would look as follows:
fn mma_with_load_and_store[M: Int, N:Int, K:Int](A: UnsafePointer[BFloat16], B: UnsafePointer[BFloat16], D:UnsafePointer[Float32]):
a = load_matrix_a[M, N, K](A, 0, 0, K)
b = load_matrix_b[M, N, K](B, 0, 0, N)
c = SIMD[DType.float32, 4](0.0)
d = SIMD[DType.float32, 4](0.0)
mma(d, a, b, c)
store_matrix_d[M, N, K](
D,
d,
0,
0,
N
)
Where 0, 0 are the coordinates of the upper left tile of the matrix we want to load.
This gives us a way to write highly performant matrix multiplication on GPUs.
I find it really nice that Mojo std provides these APIs because in CUDA we don't have an equivalent and the PTX docs only provide the pictorial description given above.
If one wanted to implement an analogous CUDA kernel in the future one could just take a look at the Mojo std and implement the equivalent code in CUDA.
Conclusion
I hope this blogpost is helpful in understanding the MMA instruction and how to implement a custom one yourself in Mojo. All the code can be found in my Github.