Outperform compiled PyTorch code using QuACK 🦆

12 Jul, 2025

Recently the QuACK library implemented highly efficient reduction methods on modern GPUs like Hopper and Blackwell. This blogpost aims to be a hands on guide how to implement new kernels using QuACK.

We will briefly explain how the RMSNorm is implemented in QuACK and show how to modify the kernel to obtain an efficient implementation of Layernorm.

RMSNorm

As the name says RMSNorm is a layer commonly used in LLMs to normalise an input. Given a matrix of shape (M, N) we simply take the slices with shape (1, N) and normalise as follows:

Y_{i, :} = \frac{1}{\sqrt{\frac{1}{n} \sum_{j = 1}^{N} X_{i, j}^{2} + ϵ}} X_{i, :} W_{i, :}

where $Y$ is row wise normalised output, $X$ is the input and $W$ is the broadcast of a vector with length like the row vectors in $X$ . Note that the kernel implementing this operation will be memory bound because reduction is a memory bound operation.

Let's see how we can implement that using the QuACK and CuTeDSL library.

The class looks as follows:

class RMSNorm(ReductionBase):
    def __init__(self, dtype: cutlass.Numeric, N: int):
        super().__init__(dtype, N, stage=1)
        self.reload_from = None if N <= 16384 else "smem"
        self.delay_w_load = False

An important parameter here is the stage. The stage determines the number of stages we need to obtain our result. In the case of RMSNorm the number of stages is equal to 1 because we only reduce once to obtain the normalisation factor. If N is large we will employ a reload from SMEM. I will further down explain how that concept works.

The call method takes three tensors: mX, mW and mO which correspond to the input, weights and output. We optionally store the rstd and provide a stream as well as the parameter epsilon for numerical stability in case $\sum_{i = 1}^{N} x_{i}^{2}$ is small.

    @cute.jit
    def __call__(
        self,
        mX: cute.Tensor,
        mW: cute.Tensor,
        mO: cute.Tensor,
        mRstd: Optional[cute.Tensor],
        stream: cuda.CUstream,
        eps: cutlass.Float32 = 1e-6,
    ):

The call simply sets up our layouts, allocates space in shared memory and the grid, block and cluster.

        assert mX.element_type == self.dtype
        assert mO.element_type == self.dtype
        self._set_cluster_n()
        tiler_mn, tv_layout = self._get_tv_layout()
        num_threads = cute.size(tv_layout, mode=[0])
        num_warps = num_threads // cute.arch.WARP_SIZE
        mW_expanded_layout = cute.prepend(mW.layout, cute.make_layout((tiler_mn[0],), stride=(0,)))
        mW = cute.make_tensor(mW.iterator, mW_expanded_layout)
        if cutlass.const_expr(mRstd is not None):
            mRstd_expanded_layout = cute.append(
                mRstd.layout, cute.make_layout((self.N,), stride=(0,))
            )
            mRstd = cute.make_tensor(mRstd.iterator, mRstd_expanded_layout)
        self.kernel(mX, mW, mO, mRstd, eps, tv_layout, tiler_mn, self.reload_from).launch(
            grid=[cute.ceil_div(mX.shape[0], tiler_mn[0]), self.cluster_n, 1],
            block=[num_threads, 1, 1],
            cluster=[1, self.cluster_n, 1] if cutlass.const_expr(self.cluster_n > 1) else None,
            smem=self._smem_size_in_bytes(tiler_mn, num_warps),
            stream=stream,
        )

The tiler and TV layout are calculated as follows:

    def _get_tv_layout(self):
        copy_bits = 128
        vecsize = copy_bits // self.dtype.width
        assert self.N % vecsize == 0, f"Input N {self.N} is not divisible by vector size {vecsize}"
        num_threads = self._get_num_threads()
        assert num_threads % cute.arch.WARP_SIZE == 0

        threads_per_row = self._calculate_threads_per_row()
        num_blocks_N = cute.ceil_div(self.N // vecsize, threads_per_row * self.cluster_n)
        cols_per_block = num_threads // threads_per_row
        tiler_mn = (cols_per_block, vecsize * num_blocks_N * threads_per_row)
        tv_layout = cute.make_layout(
            ((threads_per_row, cols_per_block), (vecsize, num_blocks_N)),
            stride=(
                (vecsize * cols_per_block, 1),
                (cols_per_block, cols_per_block * vecsize * threads_per_row),
            ),
        )
        return tiler_mn, tv_layout

Please see my past post on thread value layout and CuTeDSL on Hopper to understand it in depth. We see that essentially we want to employ vectorized loads and stores which are important to archive peak performance on modern GPUs.

Note that we will need to allocate memory for both the tensors as well as the reduction_buffer that will be used to perform the reduction.

    def _smem_size_in_bytes(self, tiler_mn, num_warps):
        return (
            cute.size_in_bytes(self.dtype, cute.make_layout(tiler_mn))
            + self.stage * num_warps * self.cluster_n * (self.reduction_dtype.width // 8)
            + self.stage * (cutlass.Int64.width // 8)
        )

The kernel signature is self explanatory.

    @cute.kernel
    def kernel(
        self,
        mX: cute.Tensor,
        mW: cute.Tensor,
        mO: cute.Tensor,
        mRstd: Optional[cute.Tensor],
        eps: cute.Float32,
        tv_layout: cute.Layout,
        tiler_mn: cute.Shape,
        reload_from: cutlass.Constexpr = None,
        delay_w_load: cutlass.Constexpr = False,
    ):

In the kernel we first setup our specifics for current Cluster, Block and Thread. We furthermore employ SmemAllocator to allocate memory.

        tidx, _, _ = cute.arch.thread_idx()
        bidx, _, _ = cute.arch.block_idx()
        if cutlass.const_expr(self.cluster_n > 1):
            cluster_y = cute.arch.block_idx()[1]
        else:
            cluster_y = cutlass.const_expr(0)

        smem = cutlass.utils.SmemAllocator()
        sX = smem.allocate_tensor(
            mX.element_type, cute.make_ordered_layout(tiler_mn, order=(1, 0)), byte_alignment=16
        )
        reduction_buffer, mbar_ptr = self._allocate_reduction_buffer_and_mbar(smem, tv_layout)

We allocate and tile tensors in GMEM.

        shape = mX.shape
        idX = cute.make_identity_tensor(shape)
        # slice for CTAs
        # We use domain_offset_i64 to deal with tensors larger than 2^31 elements
        mX, mO = [utils.domain_offset_i64((bidx * tiler_mn[0], 0), mT) for mT in (mX, mO)]
        gX, gO = [cute.local_tile(mT, tiler_mn, (0, cluster_y)) for mT in (mX, mO)]
        cX = cute.local_tile(idX, tiler_mn, (bidx, cluster_y))
        gW = cute.local_tile(mW, tiler_mn, (0, cluster_y))
        gRstd = (
            cute.local_tile(mRstd, tiler_mn, (bidx, cluster_y))
            if cutlass.const_expr(mRstd is not None)
            else None
        )

Setup copy atoms

        copy_atom_load_X = cute.make_copy_atom(
            cute.nvgpu.CopyUniversalOp(), mX.element_type, num_bits_per_copy=128
        )
        copy_atom_load_X_async = cute.make_copy_atom(
            cute.nvgpu.cpasync.CopyG2SOp(), mX.element_type, num_bits_per_copy=128
        )
        copy_atom_load_W = cute.make_copy_atom(
            cute.nvgpu.CopyUniversalOp(), mW.element_type, num_bits_per_copy=128
        )
        copy_atom_store_O = cute.make_copy_atom(
            cute.nvgpu.CopyUniversalOp(), mO.element_type, num_bits_per_copy=128
        )

        thr_copy_X = cute.make_tiled_copy(copy_atom_load_X_async, tv_layout, tiler_mn).get_slice(
            tidx
        )
        thr_copy_W = cute.make_tiled_copy(copy_atom_load_W, tv_layout, tiler_mn).get_slice(tidx)
        thr_copy_O = cute.make_tiled_copy(copy_atom_store_O, tv_layout, tiler_mn).get_slice(tidx)

Partition, i.e. compose and slice for the current thread using the copy atoms. Note that the variables follow the usual CuTe pattern where g means GMEM, s means SMEM and r means RMEM. We furthermore allocate fragments.

        tWgW = thr_copy_W.partition_S(gW)
        tXgX = thr_copy_X.partition_S(gX)
        tXsX = thr_copy_X.partition_D(sX)
        tXgO = thr_copy_O.partition_D(gO)
        tXrRstd = thr_copy_O.partition_D(gRstd) if cutlass.const_expr(mRstd is not None) else None
        tXcX = thr_copy_X.partition_S(cX)[(0, None), None, None]

        # allocate fragments for gmem->rmem
        tWrW = cute.make_fragment_like(tWgW)
        tXrW = thr_copy_X.retile(tWrW)
        tXrX, tXrO = [cute.make_fragment_like(thr) for thr in (tXgX, tXgO)]

We perform a copy under predication to take into account out of bounds due to dimensions not being perfectly divisible by corresponding block sizes. For the details I refer to utils.py.

        num_warps = cute.size(tv_layout, mode=[0]) // cute.arch.WARP_SIZE
        self._initialize_cluster(tidx, mbar_ptr, num_warps)

        tXpX = utils.predicate_k(thr_copy_X.partition_S(cX), limit=shape[1])
        row = tXcX[0][0]
        if row < shape[0]:
            cute.copy(copy_atom_load_X_async, tXgX, tXsX, pred=tXpX)
        cute.arch.cp_async_commit_group()

        tWpW = utils.predicate_k(thr_copy_W.partition_S(cX), limit=shape[1])
        if cutlass.const_expr(not delay_w_load):
            cute.copy(copy_atom_load_W, tWgW, tWrW, pred=tWpW)

Here is our core operation. We perform the the reduction. For a detailed and in depth explanation I refer to the official QuACK blogpost.

        cute.arch.cp_async_wait_group(0)
        cute.autovec_copy(tXsX, tXrX)
        x = tXrX.load().to(cute.Float32)
        threads_per_row = tv_layout.shape[0][0]
        sum_sq_x = utils.row_reduce(
            x * x,
            cute.ReductionOp.ADD,
            threads_per_row,
            reduction_buffer[None, None, 0],
            mbar_ptr,
            init_val=0.0,
            hook_fn=cute.arch.cluster_wait if cutlass.const_expr(self.cluster_n > 1) else None,
        )
        rstd = utils.rsqrt(sum_sq_x / shape[1] + eps)

We prepare the final scalings for output. Note that we perform the reload here.

        if cutlass.const_expr(mRstd is not None):
            # Only the thread corresponding to column 0 writes out the rstd to gmem
            if (
                tXcX[0][1] == 0
                and row < shape[0]
                and (self.cluster_n == 1 or cute.arch.block_idx_in_cluster() == 0)
            ):
                tXrRstd[0] = rstd
        if cutlass.const_expr(delay_w_load):
            cute.copy(copy_atom_load_W, tWgW, tWrW, pred=tWpW)
        if cutlass.const_expr(reload_from == "smem"):
            cute.autovec_copy(tXsX, tXrX)
            x = tXrX.load().to(cute.Float32)
        elif cutlass.const_expr(reload_from == "gmem"):
            cute.copy(copy_atom_load_X, tXgX, tXrX, pred=tXpX)
            x = tXrX.load().to(cute.Float32)
        x_hat = x * rstd
        w = tXrW.load().to(cute.Float32)
        y = x_hat * w
        tXrO.store(y.to(tXrO.element_type))
        tOpO = utils.predicate_k(thr_copy_O.partition_S(cX), limit=shape[1])
        if row < shape[0]:
            cute.copy(copy_atom_store_O, tXrO, tXgO, pred=tOpO)

The reload was not initially clear to me. One could think it would not have any effect on the performance because the x value is "already there". Let's benchmark the performance once with reload and once without:

With reload we will obtain 3025.00 GB/s bandwidth using a (16384, 65536) on an H100. However without reload we only obtain 2266.00 GB/s. This is significantly worse!

We can understand better by profiling a simple forward pass and run ncu on it. With the dimensions from above we can see the following difference immediately:

Without reload: Without_Reload_1 With reload: With_Reload_1

Take a look at [register/thread]. We see that in the version with Reload the register count is significantly lower.

The difference becomes even more pronounced during the reduction which can be recognised by butterfly shuffle instructions.

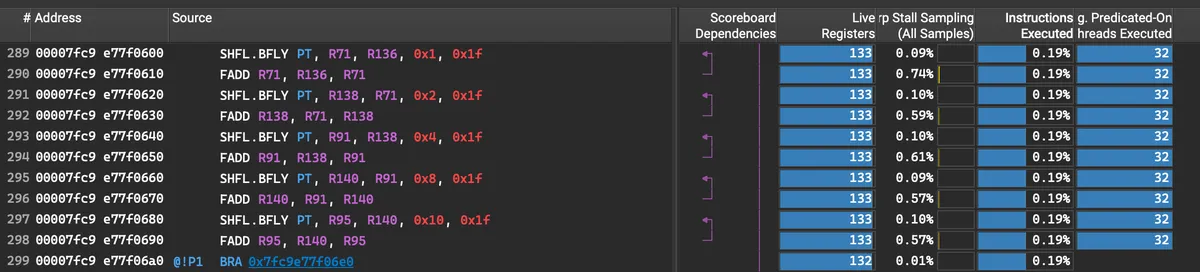
Without_Reload_2

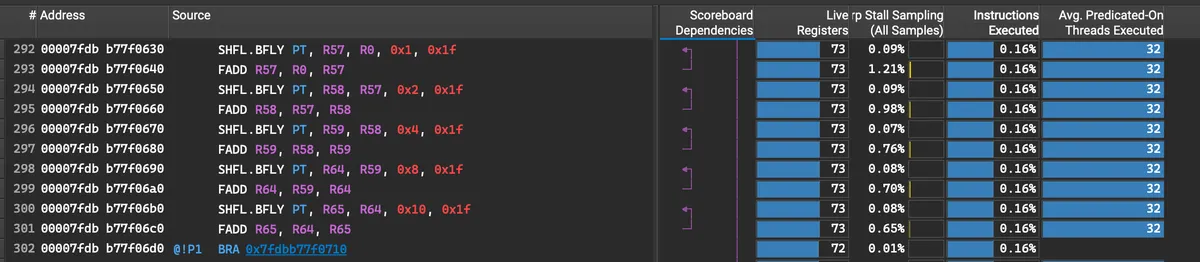
With_Reload_2

The much higher pressure on registers without reload is due to the fact, that by reloading we give the compiler a hint that we won't need x during the reduction operation. This leads to the compiler "discarding" the x registers during the reduction after we used it to calculate x*x. The reload from SMEM is cheap and the reduction is expensive. Therefore we obtain a better throughput with reload!

Layernorm

After we understood RMSNorm its actually quiet easy to write Layernorm kernel. Layernorm is similar to RMSNorm. With the same notation as above we can write it down as

Y_{i, :} = \frac{1}{\sqrt{σ_{i, :}^{2} + ϵ}} (X_{i, :} - μ_{i, :}) W_{i, :}

where $μ$ and $σ$ are the standard deviations for each row (in our notation the mean is broadcasted to match dimensions with $X$ ).

We'll see that this is a 2-stage algorithm because to variance is $σ^{2} = V (x) = E [(x - μ)^{2} (x - μ)^{2}]$ which means we need to calculate $μ$ before we can calculate $σ^{2}$ .

To implement Layernorm we therefore have

class LayerNorm(ReductionBase):
    def __init__(self, dtype: cutlass.Numeric, N: int):
        super().__init__(dtype, N, stage=2)  # 2 stages for mean and var
        self.reload_from = None if N <= 16384 else "smem"
        self.delay_w_load = False

Aside from additional mMean tensor we need in case we want to return the row wise mean the core logic needs to be updated as follows:

        sum_x = utils.row_reduce(
            x,
            cute.ReductionOp.ADD,
            threads_per_row,
            reduction_buffer[None, None, 0],
            mbar_ptr + 0 if cutlass.const_expr(self.cluster_n > 1) else None,
            init_val=0.0,
            hook_fn=cute.arch.cluster_wait if cutlass.const_expr(self.cluster_n > 1) else None,
        )
        mean = sum_x / shape[1]
        if cutlass.const_expr(reload_from == "smem"):
            cute.autovec_copy(tXsX, tXrX)
            x = tXrX.load().to(cute.Float32)
        elif cutlass.const_expr(reload_from == "gmem"):
            cute.copy(copy_atom_load_X, tXgX, tXrX, pred=tXpX)
            x = tXrX.load().to(cute.Float32)

        sum_sq_x_sub_mean = utils.row_reduce(
            (x - mean) * (x - mean),
            cute.ReductionOp.ADD,
            threads_per_row,
            reduction_buffer[None, None, 1],
            mbar_ptr + 1 if cutlass.const_expr(self.cluster_n > 1) else None,
            init_val=0.0,
        )
        rstd = utils.rsqrt(sum_sq_x_sub_mean / shape[1] + eps)
        if cutlass.const_expr(mRstd is not None):
            # Only the thread corresponding to column 0 writes out the rstd to gmem
            if (
                tXcX[0][1] == 0
                and row < shape[0]
                and (self.cluster_n == 1 or cute.arch.block_idx_in_cluster() == 0)
            ):
                tXrRstd[0] = rstd
        if cutlass.const_expr(mMean is not None):
            # Only the thread corresponding to column 0 writes out the mean to gmem
            if (
                tXcX[0][1] == 0
                and row < shape[0]
                and (self.cluster_n == 1 or cute.arch.block_idx_in_cluster() == 0)
            ):
                tXrMean[0] = mean
        if cutlass.const_expr(delay_w_load):
            cute.copy(copy_atom_load_W, tWgW, tWrW, pred=tWpW)
        if cutlass.const_expr(reload_from == "smem"):
            cute.autovec_copy(tXsX, tXrX)
            x = tXrX.load().to(cute.Float32)
        elif cutlass.const_expr(reload_from == "gmem"):
            cute.copy(copy_atom_load_X, tXgX, tXrX, pred=tXpX)
            x = tXrX.load().to(cute.Float32)
        x_hat = (x - mean) * rstd
        w = tXrW.load().to(cute.Float32)
        y = x_hat * w

We see that it is very similar to the logic above but here we reduce in 2 stages. Note that we need to update the index of the reduction buffer for each stage as well as the mbar_pointer.

To archive optimal performance we should perform a reload after each reduction to give the compiler a hint as explained above.

We can benchmark this kernel against the torch.compile version of this pytorch function:

def layernorm_ref(x: torch.Tensor, w: torch.Tensor, eps: float = 1e-6):
    x_f32 = x.float()
    return torch.nn.functional.layer_norm(x_f32, w.shape, w, None, eps).to(x.dtype)

For M = 32768, N= 8192 the two will perform comparably:

Tensor dimensions: [32768, 8192]
Input and Output Data type: BFloat16
Input tensor shapes:
x: torch.Size([32768, 8192]), dtype: torch.bfloat16
w: torch.Size([8192]), dtype: torch.float32
Executing kernel...
Kernel execution time: 0.3604 ms
Mem throughput: 2979.68 GB/s
Ref kernel execution time: 0.3593 ms
Ref mem throughput: 2988.54 GB/s

For a large N the custom QuACK kernel will vastly outperform the compiled Torch counterpart.

Tensor dimensions: [32768, 65536]
Input and Output Data type: BFloat16
Input tensor shapes:
x: torch.Size([32768, 65536]), dtype: torch.bfloat16
w: torch.Size([65536]), dtype: torch.float32
Executing kernel...
Kernel execution time: 2.9481 ms
Mem throughput: 2913.68 GB/s
Ref kernel execution time: 4.5158 ms
Ref mem throughput: 1902.18 GB/s

You can find the code here.

Conclusion

I hope this blogpost demonstrated that QuACK and CuTeDSL can be used to write highly performant kernels without much effort. To get a better understanding of QuACK I recommend their dedicated blogpost which explains the reduction mechanism in detail. The whole repo is OpenSource so you can make your own PRs and contribute further examples.