Mutual Refinement and Composition
Introduction
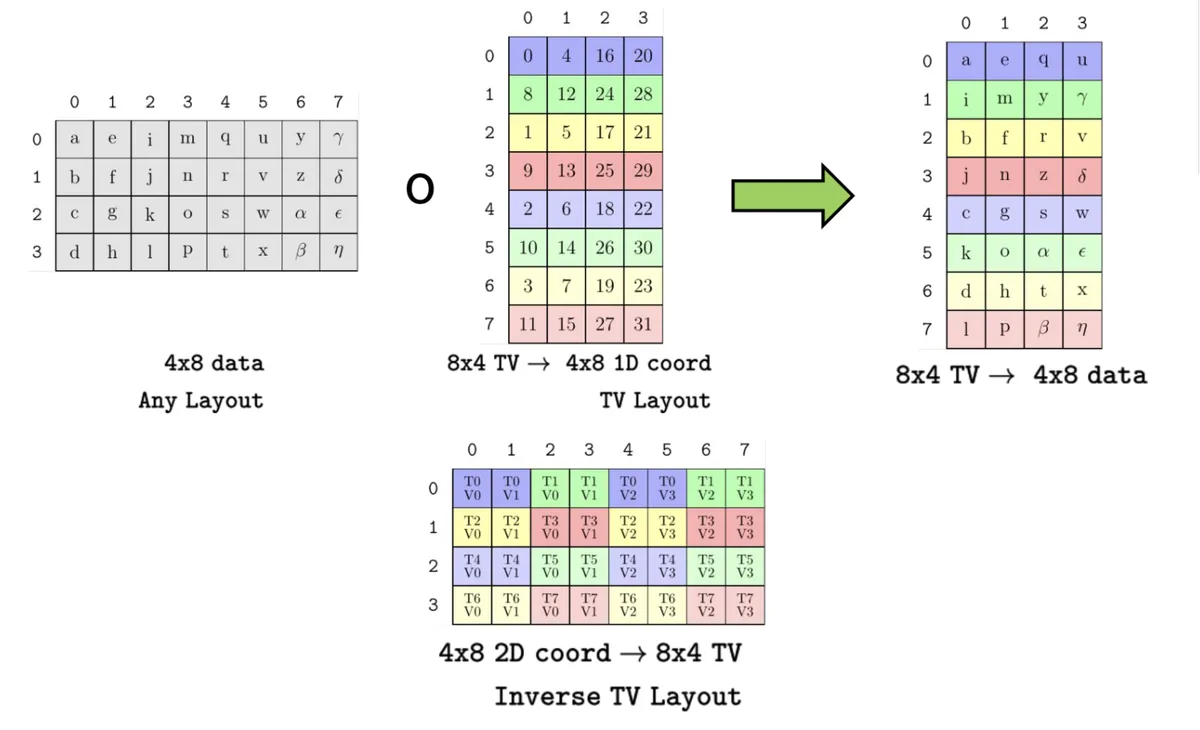
Composition is a fundamental operation on Layouts. An example one encounters for example "in the wild" is composition of data with Thread Value Layout which than gives the user possibility to assign appropriate portion of data to each thread as indicated in this picture which I took from the CuTe docs:
The categorical treatment of Layouts that Colfax established equips us with a step by step procedure to calculate Layout composition using the graphical representation of morphisms. In this blogpost I want to recap Chapter 4 of the Colfax Paper and conclude therewith my series of blogposts on this Paper.
Mutual Refinement and Composition
Consider , .
Let's find corresponding Morphism representation. Let be morphism which encodes and be morphism which encodes .
:
- , append traverse to
- , append .
- We have therefore over . :
- , append traverse to
- , append , traverse to
- , append .
- We have therefore over
This can be depicted visually:
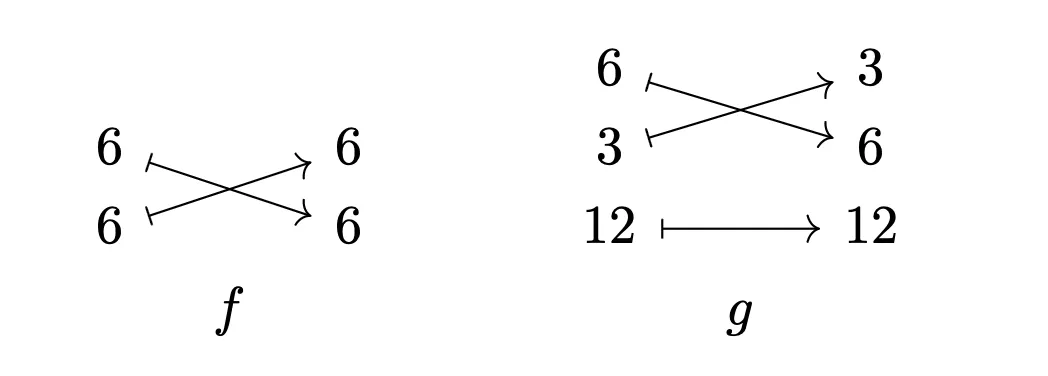
Note that we attempt to compute the Layout composition that corresponds to .
We see that is problematic, because we can't "input" the arrows coming from to the start of .
To be clear, what we want would be to have a picture like this, where arrows flow from into the domain of and from there into the codomain of . We see below that loosely speaking that is archived by splitting up the into a and a in the codomain of and by factoring the in the domain of into and .
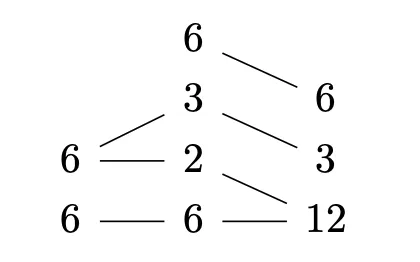
Here we see the concept visually.
Let's recap the concept of Refinement. refines refines but not in the other direction. That is because in our framework Refinement can be thought of such that refines if may be obtained from by replacing each entry in with a some nested tuples of equal size. Let us think a moment about what this geometrically means using a simple example:
can be geometrically thought of as a rectangle. also describes shape of a rectangle. However one dimension of a rectangle can be again described as a rectangle. This is useful and important concept in CuTe because it allows us to implement highly non trivial patterns in an intuitive way as you can convince yourself of by following examples from my blogpost about hierarchical Layouts.
A mutual refinement can be thought of in terms of the following diagram

In other words we want to refine the codomain of one function and the domain of another function such that we all possible values of the codomain of one function lie in the domain of the other function. That in turn will yield that we can compose the two functions we obtain by mutually refining.

This is an algorithm to find mutual refinement between two nested tuples.
Let's apply it to and .
Initially we have . We will now compute the mutual refinement .
Note that and .
First step:
- divides
- , ,
- divides , ,
- , ,
- ,
- , ,
Fill Y' with remaining entries from Y
So we obtained and
The diagram on the left show
T' U'
T U
We know that the domain of the second morphism needs to contain the codomain of the first morphism (after all, that is the whole reason we perform mutual refinement) which is depicted by the fact that for the upper we only have an outgoing arrow. For all the other entries we have ingoing and outgoing arrow.
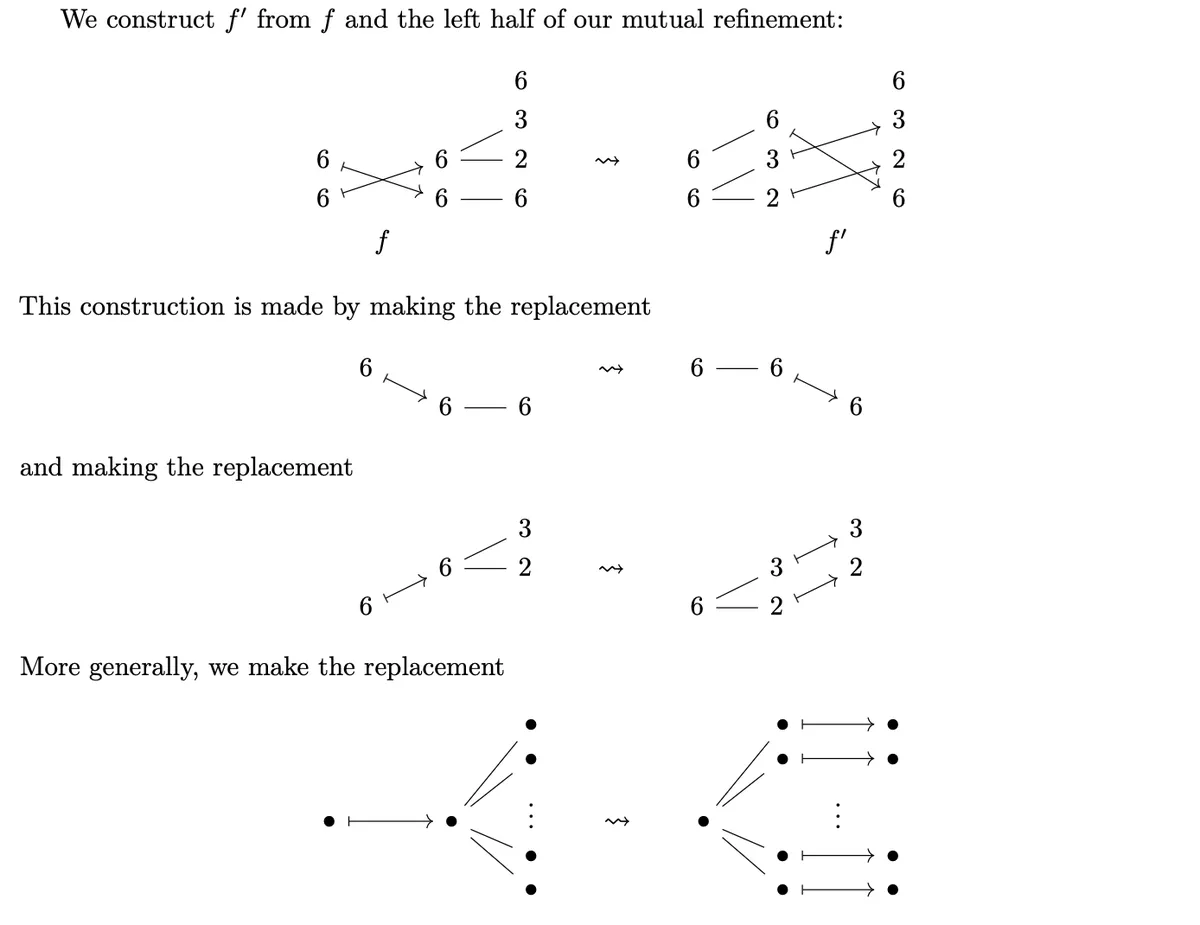
Note that we take all "branching arrows" at the second stage and instead branch at first stage and than have an "identity arrow" pointing from .
Here we simply make the replacement that for every incoming branch we replace it with a simple identity onto itself .
Let's take a look again at the above diagram and show how to resolve the diagram:
The left side is obtained by the process provided above.
- Find mutual refinement.
- Bring each part separately into the desired form by using above process Gives us the left side.
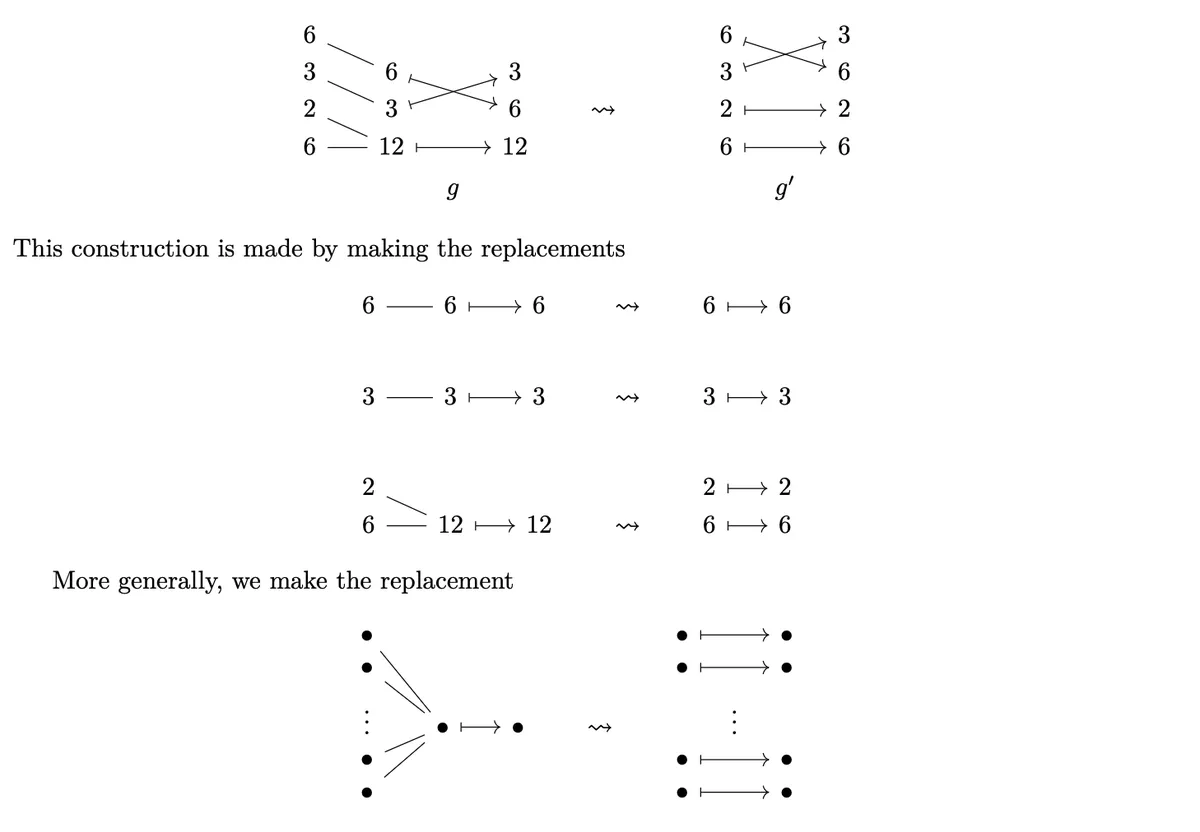
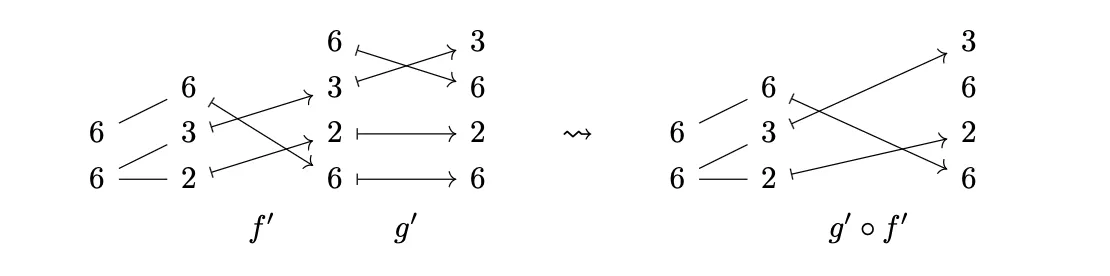
From here we can drop the "mutual refinement" layer from the middle because by construction it is clear that from left and right side. This gives us the right diagram from where we can read of over .
This in return yields the Layout:
- equip stride with profile
We have a useful theorem that connect the composition to .
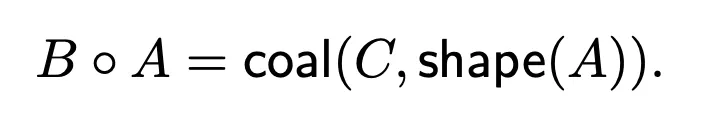
So to obtain the composition we just take the complement of .
That means we have a clear procedure to compute composition:
- Determine standard representation of and
- Determine mutual refinement similar to what we did above
- Form the diagram using mutual refinement, i.e. "connect" codomain of and domain of to the mutual refinement "layer"
- Use above mechanism to resolve the diagram. For incoming branches, let them branch from their corresponding source and from there map . For outgoing branches map instead of branching "into" a source
- Read off the Layout from the diagram
- Use the above formula to obtain the composition from the Layout we read off the diagram. (i.e. coalesce over the size of the Layout we apply first)
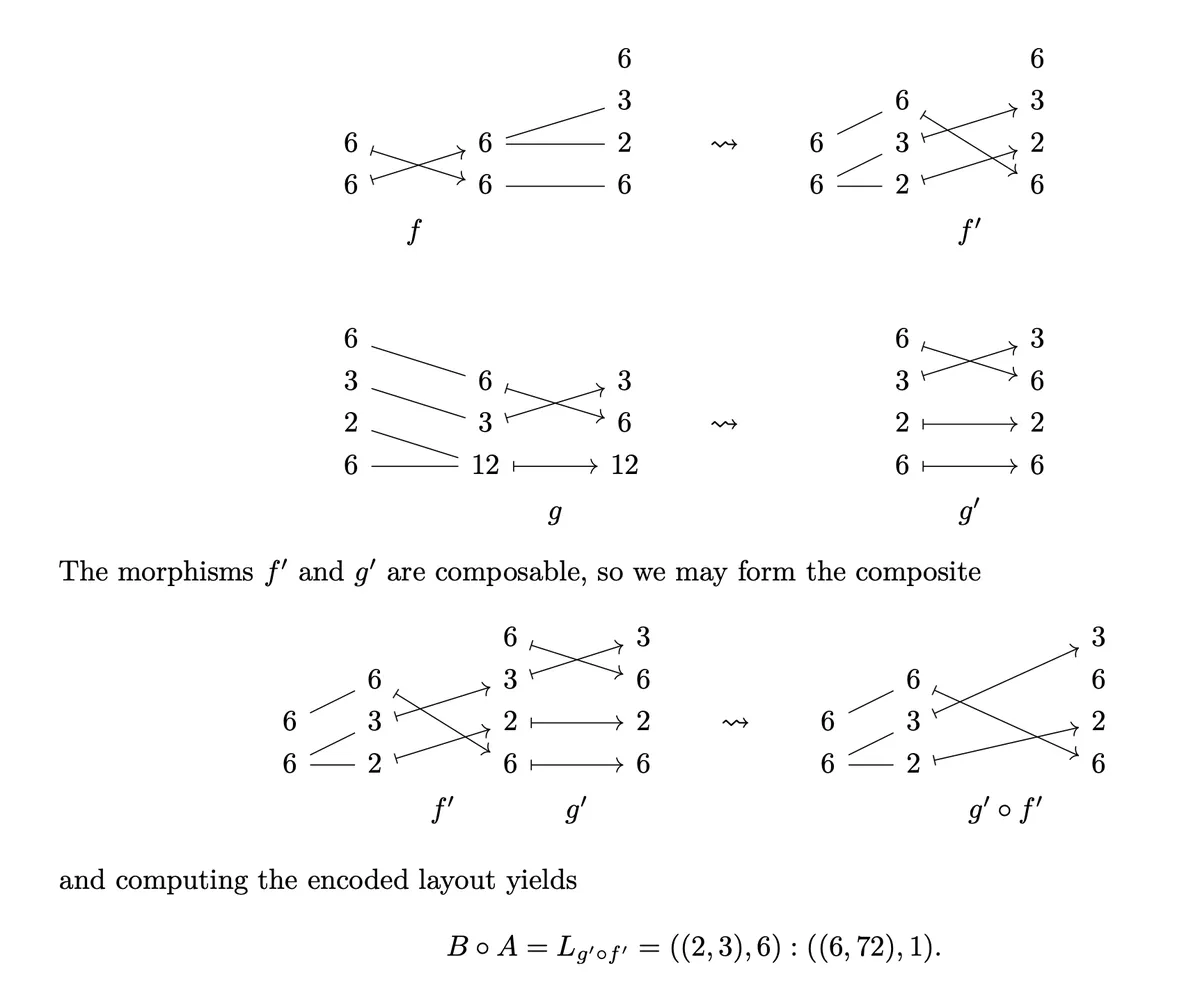
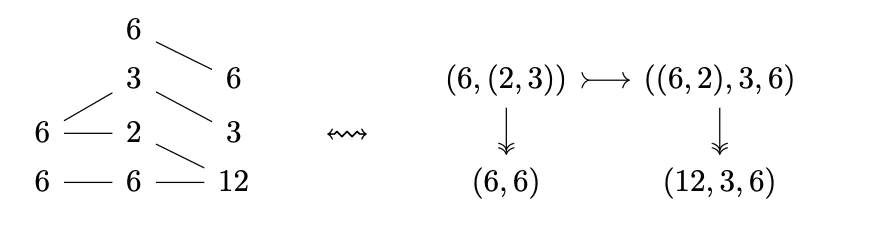
Let's use the most complex example given in the Paper and analyse it step by step:
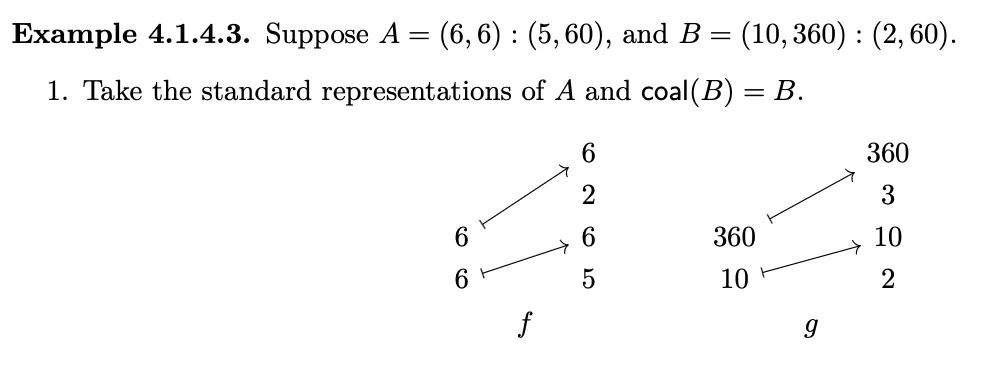
- We see that corresponds to because and .
- We see that corresponds to and .
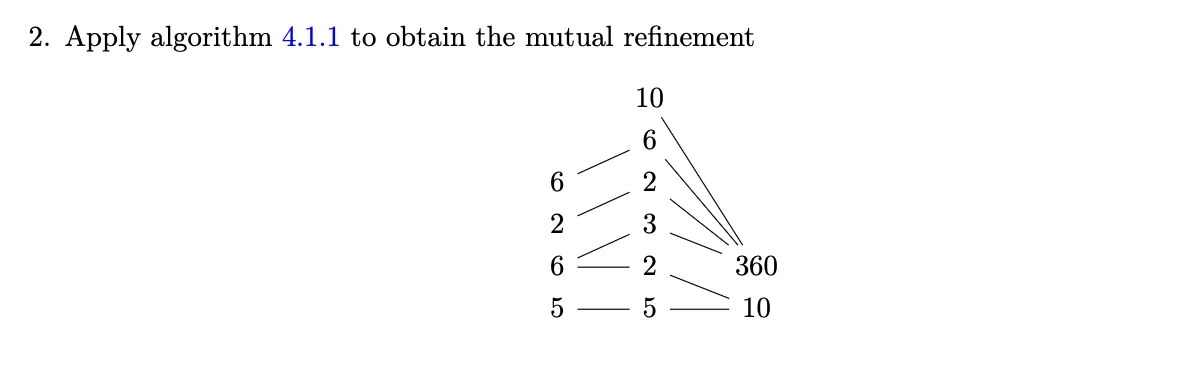
- We will not go through the mechanical procedure above, but we can confirm visually that this is correct. We see that , and .
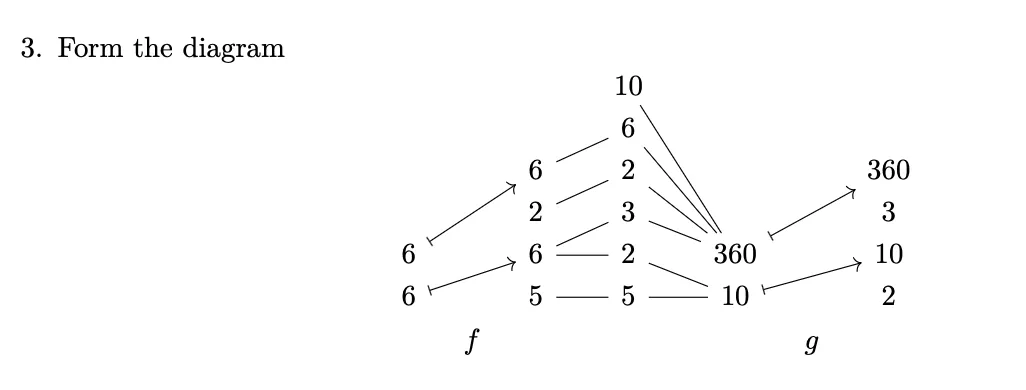
- Forming the diagram here means simply to insert the "mutual refinement layer" in the middle and connect the codomain of to it and the domain of to it.
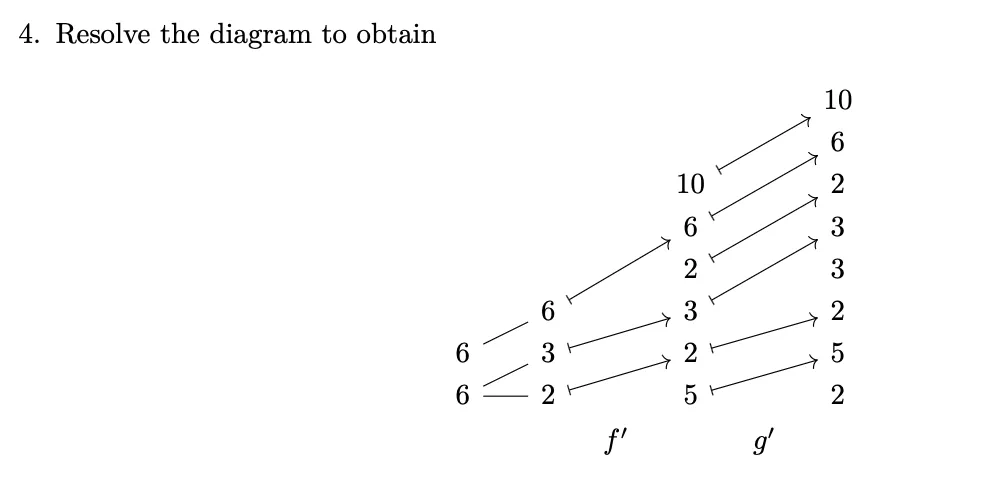
- Resolving the diagram is the process from above.
- Left side of mutual refinement layer: For example replace by the two points it branches to ( and ) and map them via .
- Right side: This is even simpler. Simply "resolve" all branches via .
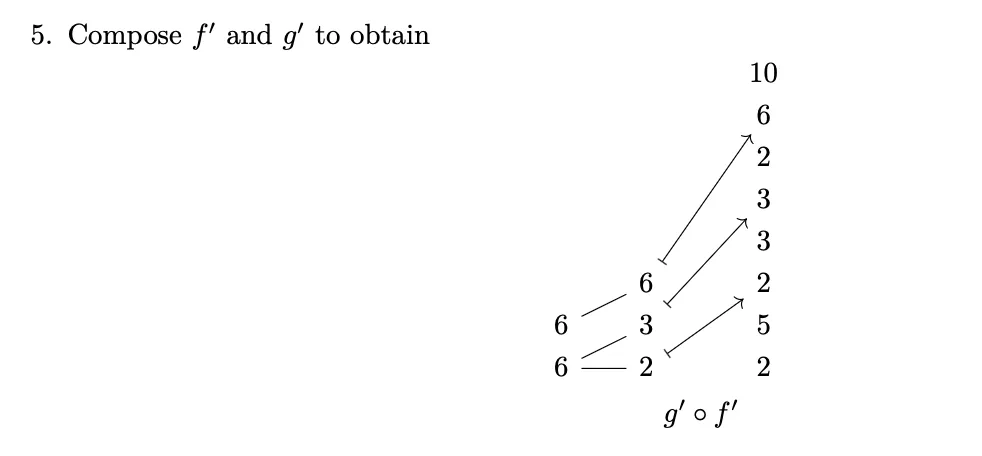
- We remove the "mutual refinement layer". This is can be easily done by tracing from where the three arrows entering come and where they go to. For example goes into at and from there to so we can replace the two arrows by one arrow directly going from to and similar for the others.
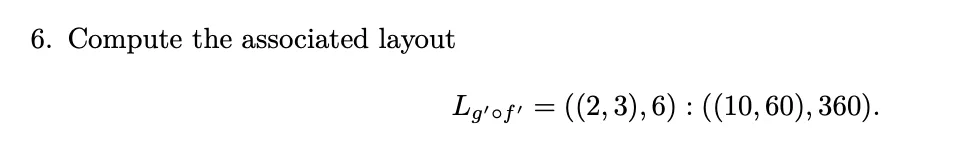
- Read the Layout off
- flattened stride is (see above how to obtain it)
- is the flattened stride equipped with profile of the shape.
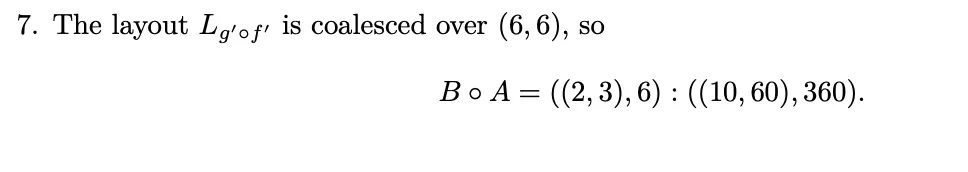
- The relative modes and are coalesced, therefore the Layout is coalesced over the shape and we are done. The relative modes are determined by the procedure described in Relative coalesce chapter of the paper.
Conclusion
This concludes the blogpost about the Colfax paper. Please consider starring the repository they released along the paper. The codebase delivered there offers also ability to produce lots of the figures shown here and of course can be used to let computer perform the calculations. However it is helpful if we know how things supposed to look like so we can sanity check the computer output and especially understand how to interpret them.