Layout Gymnastics

23 Sep, 2025

Introduction

Colfax recently released an excellent Paper on CuTe Layouts. In this note I calculated many of the examples of Chapter 2 by hand. I hope this can can be a small complement to the original paper to show the various formulas in action and give a step by step solution to many examples for even better accessibility. Please refer to the original Paper for more the whole theory as the selection I made is obviously not complete.

Learning Notes

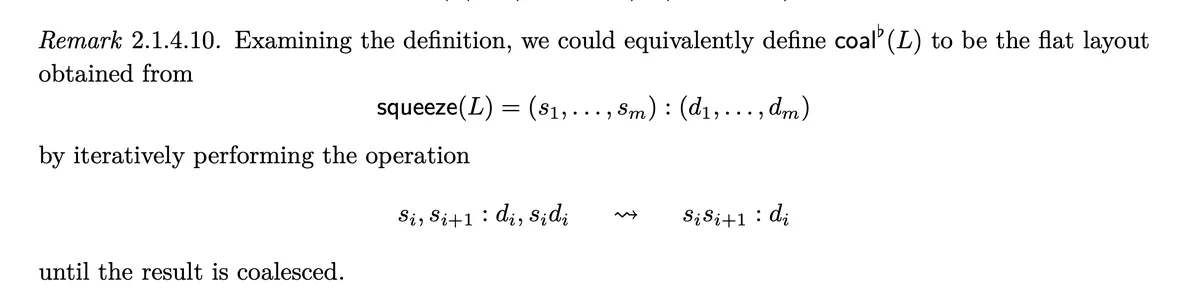
• Modes with $s_i$ are redundant because they are the map $0\to 0$ and therefore don't contain any information
• $(s_i,s_{i+1}):(d_i,d_i{s}_i)$ obey $\phi (x_1,x_2)=x_1{d}_i+x_{i+1}{d}_i{s}_i=(x_i+x_{i+1}{s}_i)d_i$. Note that $x_{i+1}\in \{1,...,s_{i+1}\}$ and therefore $x_{i+1}{s}_i=\in \{s_i,...,s_i{s}_{i+1}\}$ and with $x_i\in \{1,...,s_i\}$ it follows that $x_i+x_{i+1}{s}_i\in \{1,...,s_i{s}_{i+1}\}$ from where we can conclude that we can replace the two modes by one mode $(s_i{s}_{i+1}):(d_i)$.

$L=(2,2,2,2,2):(8,16,1024,2048,4096)$

• $(2,2,2,4):(8,16,1024,2048)$, last two modes
• $(2,2,8):(8,16,1024)$, last two modes
• $(4,8):(8,1024)$, first two modes

$L=(3,4,1,5):(1,8,3,32)$

• $(3,4,5):(1,8,32)$, squeeze
• $(3,20):(1,8)$ last two modes

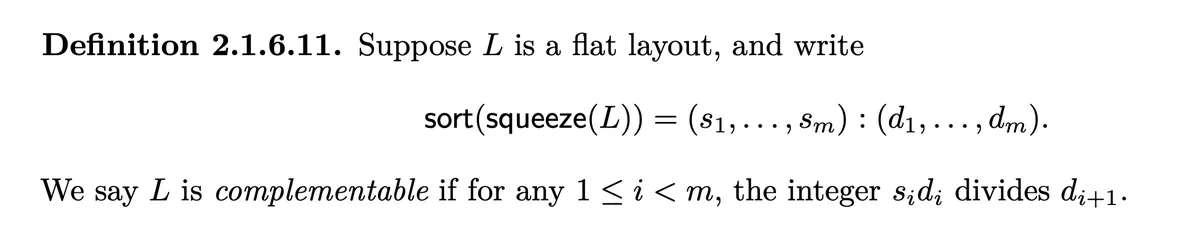
• If we would have that $s_i{d}_i$ does not divide $d_{i+1}$ we'd have a "jump" within the Layout which could not be filled up by a regular placement in the slots between.

$L=(4,1,1,4,4):(64,0,0,1,8)$

• $\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L)=(4,4,4):(64,1,8)$
• $\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}(\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L))=\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}((4,4,4):(64,1,8))=(4,4,4):(1,8,64)$
• $s_1{d}_1=4$ divides $d_2=8$ and $s_2{d}_2=32$ divides $d_3=64$, therefore $L$ is complementable.

$L=(4,4,4):(64,1,1)$ is not complementable because $\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}(\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L))=(4,4,4):(1,1,64)$ and $s_1{d}_1=4$ does not divide $1$.

• $C$ is a Layout that fills out the holes between the modes of the $\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{e}\mathrm{d}$ Layout.

$L=(8,8):(1,8)$

• $C=(1,\frac{8}{8}):(1,8)=(1,1):(1,8)$
• ${\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}^{♭}(C)={\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}}^{♭}(C)=()$

Note that $L$ is compact which means that ${\Phi }_L^{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(L)}$ is an isomorphism (see 2.1.5.1). That in return leads to the complement being the empty Layout because there are no "holes to fill". This is also clear from 2.1.6.9 because we define the complement to be precisely that Layout that gives us a compact Layout when concatenated with the Layout it complements.

$L=(2,2):(2,8)$

• $C=(2,\frac{4}{2}):(1,4)=(2,2):(1,4)$
• ${\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}^{♭}(C)={\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}}^{♭}(C)=C=(2,2):(1,4)$

$L=(3,3,8):(16,96,1)$

• $\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}(\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L))=(8,3,3):(1,16,96)$
• $C=(1,2,2):(1,8,48)$
• ${\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}^{♭}={\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}}^{♭}(C)=(2,2):(8,48)$

If $\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(\mathrm{L})·\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}({\mathrm{L}}^{\mathrm{\prime }})=N$ where $L^{\prime }$ is the complement to $L$ we say that $L^{\prime }$ is an $N$ complement of $L$.

$L=(2,2):(2,8)=\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}(\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L))$

• $s_1{d}_1=4$ divides $d_2=8$, $s_2{d}_2=16$ so $L$ is $16,32,48,...$ complementable.

$L=(3,10):(80,4)$, $N=2400$

• $\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}(\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L))=(10,3):(4,80)$
• $C=(4,2,10):(1,40,240)$
• ${\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}^{♭}(L,N)={\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}}^{♭}(C)=(4,2,10):(1,40,240)$

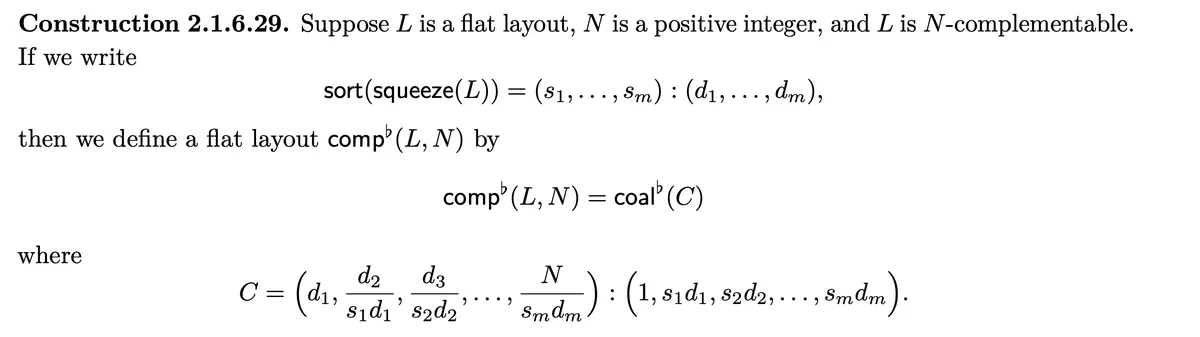An example:

Note that we simply multiply the strides with the stride of $B$.

Consider the Layout $A=(s_1,s_2):(0,0)$. The strides of $0$ means that ${\Phi }_A(x)=0$ for all $x\in \{1,...,s_1{s}_2\}$. If we compose such a Layout with Layout $B$ than we have $B\circ A=A$ because all elements will get mapped to $0$ and $0$ will get mapped by any Layout function ${\Phi }_B$ to $0$.

Consider composition with the Layout $B=(2048,2048):(1,2048)$. Compose with Layout $A=(64,32):(2,256)$. We have that $\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(A)=1+{\sum }_{i\in \{1,2\}}(s_i-1)d_i=1+63·2+31·256=8063$. Let ${\Phi }_A(x)=k$ with $0\le k\le 2047$ than ${\Phi }_B(k)=k$. Let ${\Phi }_A(x)=2048+k$ than ${\Phi }_B(2048+k)\to (k,1)\to k+2048$. Similar ${\Phi }_B(4096+k)\to (k,2)\to k+4096$ and ${\Phi }_B(6144+k)\to (k,3)\to k+6144$ (where in the last case of course we have that $maxk+6144=8063$ because that is the cosize of $A$. Thus we have that ${\Phi }_B$ is the identity on the image of ${\Phi }_A$. That would not necessarily be the case if the strides of $B$ would be different.

Consider the composition $B=(2,2,6):(12,6,1)$ and $A=(4):(2)$ than we have

$0\to (0)\to 0\to (0,0,0)\to 0$ $1\to (1)\to 2\to (0,1,0)\to 6$ $2\to (2)\to 4\to (0,0,1)\to 1$ $3\to (3)\to 6\to (0,1,1)\to 7$

We see that there is no flat layout $R=(4):(d)$ than can have such a Layout function so we can't compose arbitrary Layouts.

For example:

$Q=(*,*),P_1=(*,*),P_2=(*,*,*)$

This leads to $(P_1,P_2{)}_Q=((*,*),(*,*,*))$.

Congruence means that the profiles of two nested tuples agree. $(2,(2,2))$ is compatible with $(1,(2,3))$ but not compatible with $(1,2,3)$.

For example let $(X_1,X_2,X_3)=((1,2,3),4,(5,6))$ and $Q=(*,(*,*))$ than we have $(X_1,X_2,X_3{)}_Q=((1,2,3),(4,(5,6)))$. A special case is $Q=(*,*,...,*)$ which is just the concatenation of $X_1,...,X_m$.

Note that $8$ is a refinement of $(2,(2,2))$ because we have $\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(8)=8=2·2·2=\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}((2,(2,2))$. For $((2,2),(3,3),(5,5))$ we have that the $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}$ is equal to $3$ and each of the modes is a refinement of the corresponding other modes, i.e. $4$ is a refinement of $(2,2)$ because $\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(4)=4=2·2=\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}((2,2))$ etc.

Note that $(2,(4,8)):(1,(8,4))$ is a Layout but $(2,(4,8)):(1,32)$ is not. That is because in the second example $S=(2,(4,8))$ has a different profile (namely $(*,(*,*))$) than $D$ (namely $(*,*)$).

For example $L=(2,(4,8)):(1,(8,4))$ has:

• $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}(\mathrm{L})=2$
• $\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}(L)=3$
• $\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{h}(L)=2$
• $\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(L)=2·4·8=64$
• $\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{f}(L)=(*,(*,*))$

The flattening of a Layout flattens the nested tuple into ordinary tuple, i.e. $L^{♭}=S^{♭}:D^{♭}$. For the above example we have $L^{♭}=(2,4,8):(1,8,4)$.

The Layout function is given by ${\Phi }_L={\Phi }_{L^{♭}}$.

Let's consider $L=((2,2),2):((3,0),10)$, than we have $L^{♭}=(2,2,2):(3,0,10)$ which gives us

$0\to (0,0,0)\to 0$ $1\to (1,0,0)\to 3$ $2\to (0,1,0)\to 0$ $3\to (1,1,0)\to 3$ $4\to (0,0,1)\to 10$ $5\to (1,0,1)\to 13$ $6\to (0,1,1)\to 10$ $7\to (1,1,1)\to 13$

Not associative, because for example $L_1=3:4$, $L_2=2:2$, $L_3=5:1$. We have $(3,(2,5)):(4,(2,1))\ne ((3,2),5):((4,2),1)$ because they have different profiles. However the Layout function is the same because when flattened they are equal and the Layout function of nested tuples is defined by the flattened Layout.

The substitution won't affect the Layout function, however it will change the interpretation. To see that consider:

$L=(2,2,2):(1,2,4)$ which is a cube. However $L_P=((2,2),2):((1,2),4)$ is a plane!

L'
       0 1
(0, 0) 0 4
(1, 0) 1 5
(0, 1) 2 6
(1, 1) 3 7

$L=((2,2,2),(5,5)):((1,2,4),(10,50))$:

• $L^{♭}=(2,2,2,5,5):(1,2,4,10,50)=\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{e}\mathrm{d}(\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L))$
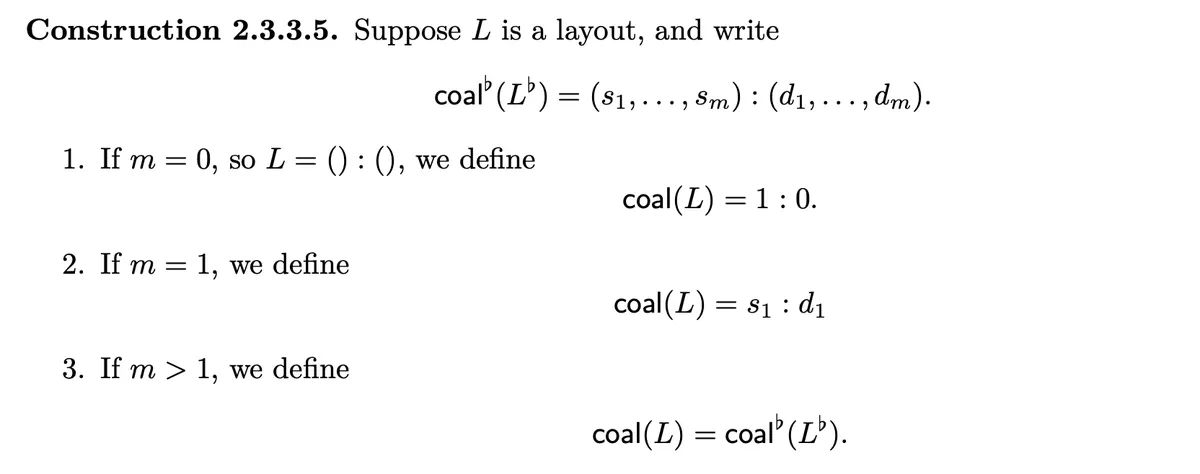
• $(2,2,2,25):(1,2,4,10)$ combine last two modes
• $(2,4,25):(1,2,10)$ combine second and third mode
• $(8,25):(1,10)$ combine first two modes

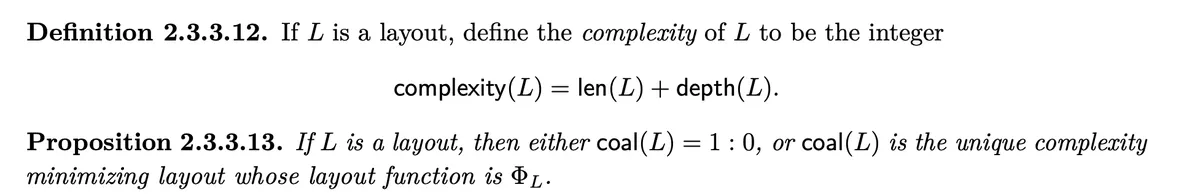
Note that this is intuitively clear.

$S^{\prime }=(4,(9,25))$, $L=((2,2),((3,3),(5,(1,5)))):((1,2),((6,18),(90,(0,450))))$

Note that $4$ corresponds to $(2,2)$, $9$ corresponds to $(3,3)$ and $25$ corresponds to $(5,(1,5))$. From here we get the above relative modes.

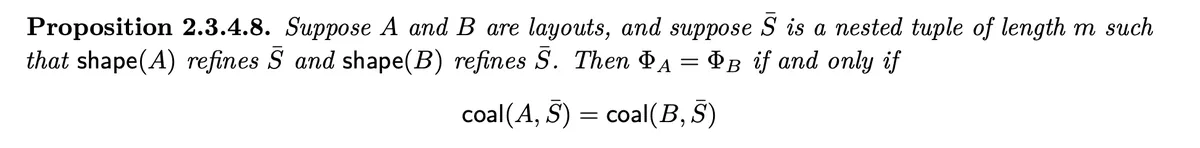
That makes it easy to determine compactness of hierarchical Layouts, for example $L=(2,(2,2)):(1,(2,4))$ is compact because $L^{♭}=(2,2,2):(1,2,4)$ is column major and therefore compact.

$L=((4,2),(2,2)):((3,24),(192,96))$, $L^{♭}=(4,2,2,2):(3,24,192,96)$. Let us calculate the N complement for $N=768$:

• $\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}(\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L^{♭}))=(4,2,2,2):(3,24,96,192)$. We see that $s_i{d}_i$ divides $d_{i+1}$ for $i<4$ and $s_4{d}_4$ divides $768$. Therefore we can calculate the complement.
• $C=(3,2,2,0,2):(12,48,192,384)$
• ${\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}^{♭}(L^{♭},N)={\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}}^{♭}(C)=(3,2,2,2):(12,48,192,384)$
• $\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}(L,N)=\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}({\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}^{♭}(L^{♭},N))=(3,2,2,2):(12,48,192,384)$

$L=((16,4),64):((1,16),64)$ and $N=8192$

• $\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}(\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L^{♭}))=(16,4,64):(1,16,64)$. We see that $s_i{d}_i$ divides $d_{i+1}$ for $i<3$ and $64$ divides $8192$
• $C=(1,1,2):(16,64,4096)$
• ${\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}^{♭}$ will remove the redundant first modes
• Therefore $\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}(L,N)=\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}((2):(4096))=2:4096$.

$A=(4):(2)$ and $B=(2,2,6):(12,6,1)$

${\Phi }_A$ is given by ${\Phi }_A(x)=2x$ for $x\in \{0,1,2,3\}$ We have that

• $0\to (0,0,0)\to 0$
• $2\to (0,1,0)\to 6$
• $4\to (0,0,1)\to 1$
• $6\to (0,1,1)\to 7$ We can identify that such

(0,0) 0
(1,0) 6
(0,1) 1
(1,1) 7

which is $((2,2)):((6,1))$. Obviously $((2,2))$ refines $(4)$ because $2·2=4$. Furthermore the Layout is coalesced because $(2,2):(1,6)$ is clearly coalesced. Note we could have not expressed this via flat layouts.

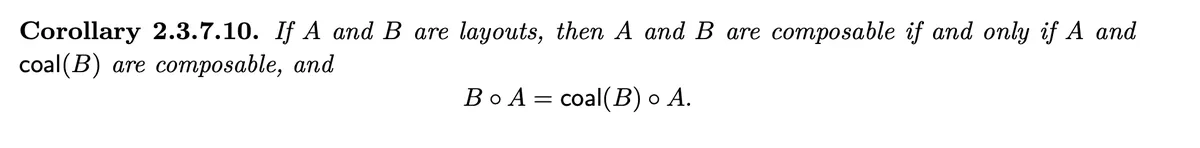
This gives a condition on composability.

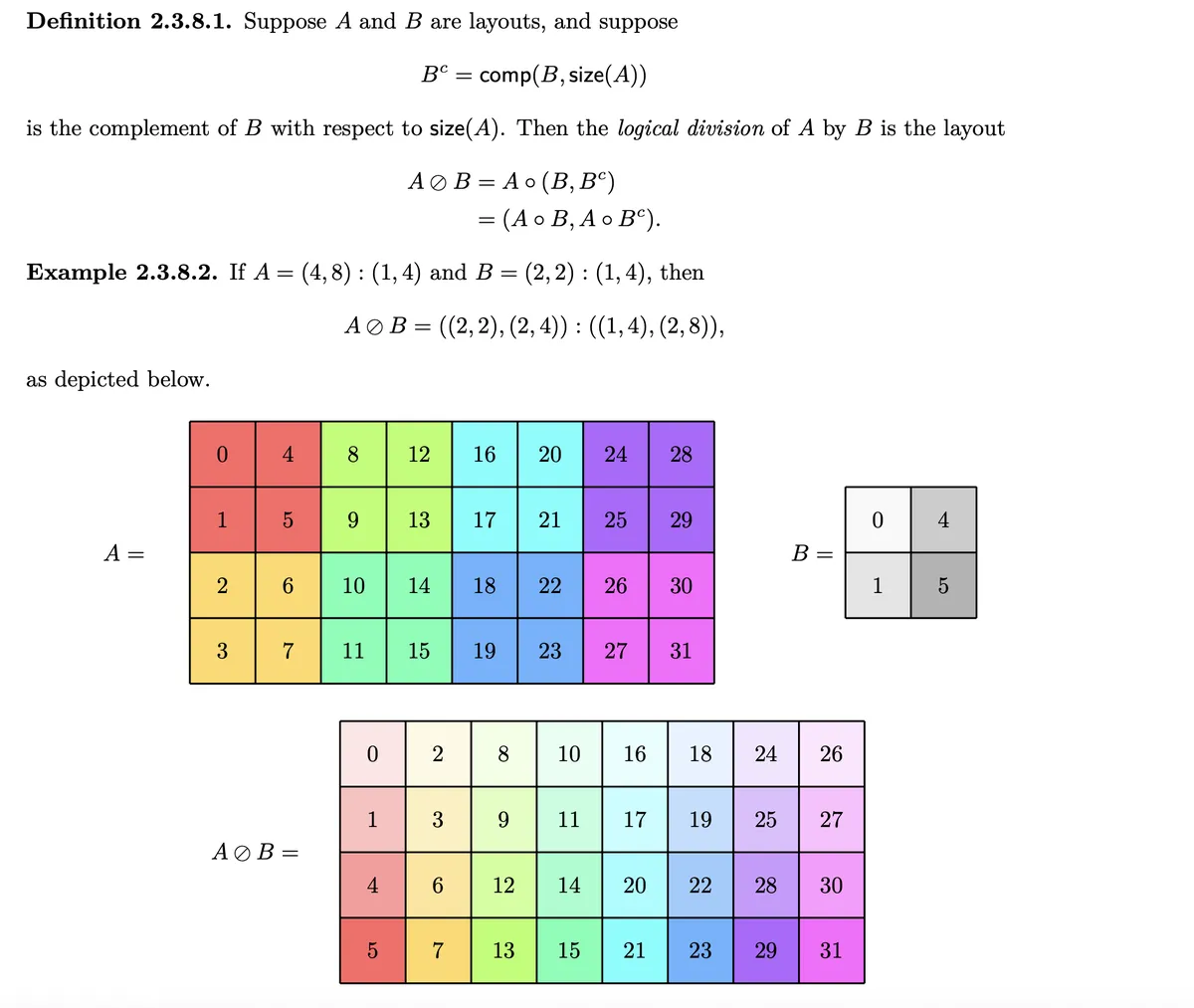
Intuition: $B^c$ is the $\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(A)$ complement of $B$. Note that this means that $B^c$ "hits" the holes $B$ has in $\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(A)$. Therefore $B^c$ in the second mode will give us an index in the corresponding subtile of $\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(B)$. The motivated reader may derive the above Layout "by hand" using the calculation techniques we used above.

Conclusion

I hope this can serve as a complementary guide to the original chapter 2 by making many of the examples explicit and giving step by step solution. I am exited about the new way of looking at Layout algebra offered in chapter 3 and 4 and will hopefully publish further posts on this topic in the future. Please consider starring the Github repo that comes with the Colfax paper.