Infinite binary strings

09 Jun, 2025

We call $\mathbf{\text{B}}=\{\mathit{\text{0}},\mathit{\text{1}}\}$ the binary alphabet. ${\mathbf{\text{B}}}^{\infty }$ is the set of infinite binary strings $\omega ={\omega }_{1:\infty }={\omega }_1{\omega }_2{\omega }_3...$ with ${\omega }_i\in \mathbf{\text{B}}$.

We can identify each of these strings with a number in the unit interval $[0,1]$ in the following way:

This maps each infinite binary string to the real number with binary expansion $0.{\omega }_1{\omega }_2{\omega }_3...$ .

We can draw a similarity between infinite binary trees and the task of finding the binary expansion of a number:

The tree corresponding to finding one of the binary expansions of $\frac{1}{4}$ would look as follows:

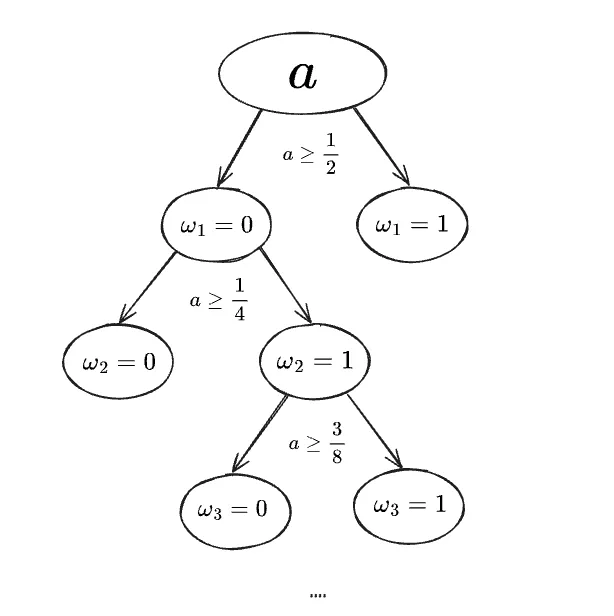
... at the end means that we infinitely expand the tree further down.

In the picture we just show one possible path to obtain $\frac{1}{4}=0.01000...$

Note that this picture already hints at the fact that the binary expansion is not injective. We can read off two possible binary expansions of $\frac{1}{4}$:

The function is $f$ is surjective because for every number in the interval $[0,1]$ we can apply the above algorithm to find an infinite binary expansion that will match it.

The real numbers $\mathbf{\text{R}}$ have geometrical representation of a straight line.

We can similarly visualise ${\mathbf{\text{B}}}^{*}$ using the cylinder sets.

Here $x\in {\mathbf{\text{B}}}^{*}$, i.e. a finite binary string.

We can than visualise ${\Gamma }_x$ as the interval $f({\Gamma }_x)$, for example ${\Gamma }_{ϵ}$ will correspond to the whole unit interval, ${\Gamma }_{\mathit{\text{1}}}$ to the interval $[\frac{1}{2},1]$, ${\Gamma }_{\mathit{\text{11}}}$ to the interval $[\frac{3}{4},1]$, ${\Gamma }_{\mathit{\text{000}}}$ to the interval $[0,\frac{1}{8}]$ etc.

We call $x\in {\mathbf{\text{B}}}^{*}$ a prefix of $y\in {\mathbf{\text{B}}}^{*}$ if we have $xz=y$ for $z\in {\mathbf{\text{B}}}^{*}$.

Let's prove that ${\Gamma }_y\subset {\Gamma }_x$ iff $x$ is a prefix of $y$.

$\to$: We have for arbitrary $\alpha \in {\Gamma }_y$ that $\alpha \in {\Gamma }_x$. That implies that for each $y\omega$ we can find $x{\omega }^{\prime }$ such that $y\omega =x{\omega }^{\prime }$. We have $l(x)\le l(y)$ because if $l(x)>l(y)$ we would have elements in ${\Gamma }_y$ that are not in ${\Gamma }_x$. We can than compare the substrings $(y\omega {)}_{1:l(x)}=y_{1:l(x)}$ and $(x{\omega }^{\prime }{)}_{1:l(x)}=x$. They need to be equal and from here it follows that $x$ is a prefix of y.

$\leftarrow$: We have that $xz=y$ but than we can write $y\omega =xz\omega$ and hence every element of ${\Gamma }_y$ is in ${\Gamma }_x$.

This concludes the proof and can be geometrically interpreted as the fact that iff $x$ is a prefix of $y$ than $f({\Gamma }_y)$ is a subinterval of $f({\Gamma }_x)$.