Epilogue in CuTeDSL H100 kernels
Here and below we will run
uv run dense_gemm.py \
--mnkl 4096,1024,2048,1 --tile_shape_mnk 128,256,64 \
--cluster_shape_mn 1,1 --a_dtype Float16 --b_dtype Float16 \
--c_dtype Float16 --acc_dtype Float32 \
--a_major k --b_major k --c_major n
if not mentioned otherwise.
Before starting to analyse the Epilogue let's take a look at
tiled_mma = sm90_utils.make_trivial_tiled_mma(
self.a_dtype,
self.b_dtype,
self.a_layout.sm90_mma_major_mode(),
self.b_layout.sm90_mma_major_mode(),
self.acc_dtype,
self.atom_layout_mnk,
tiler_mn=(64, self.tile_shape_mnk[1]),
)
Tiled MMA
Thr Layout VMNK: (128,2,1,1):(1,128,0,0)
Permutation MNK: (_,_,_)
MMA Atom
ThrID: 128:1
Shape MNK: (64,256,16)
TV Layout A: (128,(64,16)):(0,(1,64))
TV Layout B: (128,(256,16)):(0,(1,256))
TV Layout C: ((4,8,4),(2,2,32)):((128,1,16),(64,8,512))
Short reminder of derivation:
See below picture
Thread Layout = (4,8,4):(128,1,16).
(T0,d0) -> (T1,d0) = 128 steps and 4 in one column, (T0,d0) -> (T4,d0) = 1 step and 8 in one color row, (T0,d0)->(T32,d0) = 16 steps and 4 colors. This fully describes the Thread layout.
Value Layout = (2,2,32):(64,8,512).
(T0,d0) -> (T0,d1) = 64 steps and 2 in one column, (T0,d0) -> (T0, d2) = 8 steps and 2 in one row. Than we repeat N / 8 = 256 / 8 = 32 times and from (T0,d0) -> (T0, d4) = 64 * 8 = 512 steps.
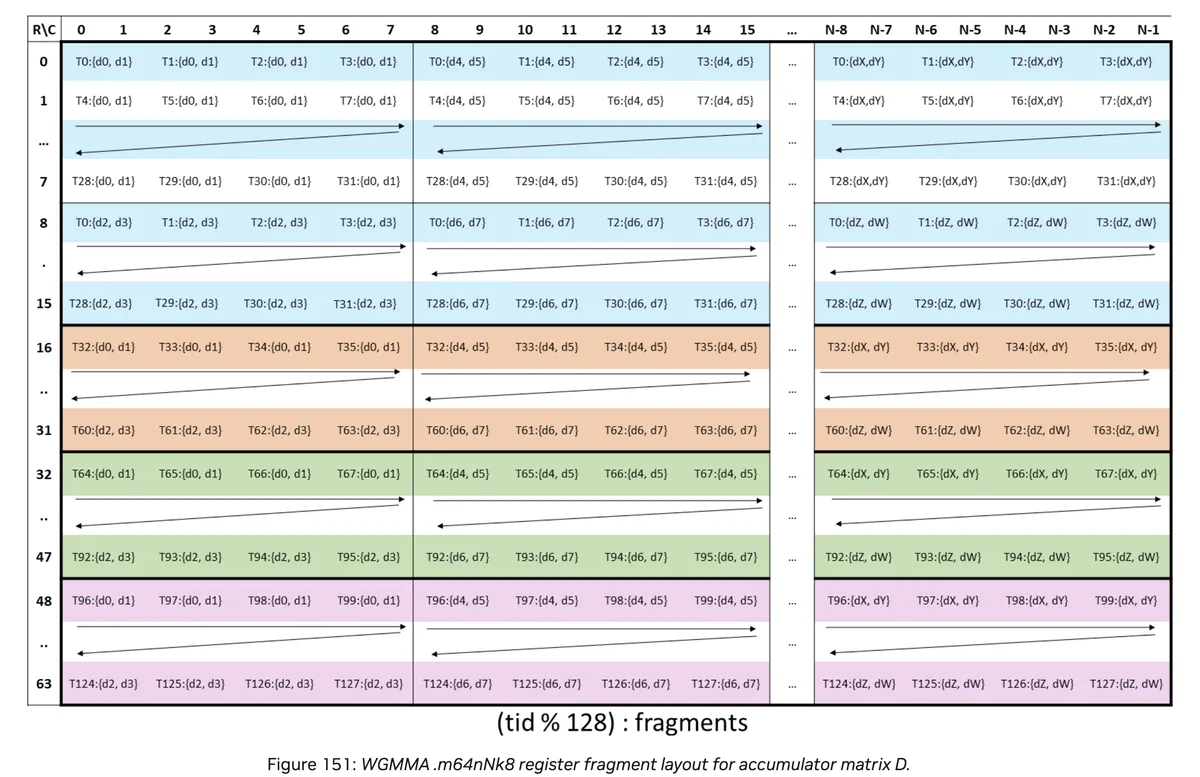
Note that per thread we provide 64 * 256 / 128 = 128 = 2 * 2 * 32 register values to the wgmma instruction.
In the mainloop we perform the GEMM per tile and within each tile we split the tile into further subtiles because wgmma instruction has dimension 16 along K dimension and our tilesize in K dimension is larger than that. We accumulate the result into accumulators.
for k_tile in cutlass.range(k_pipe_mmas, k_tile_cnt, 1, unroll=1):
...
for k_block_idx in cutlass.range(num_k_blocks, unroll_full=True):
...
cute.gemm(
tiled_mma,
accumulators,
tCrA_1phase,
tCrB_1phase,
accumulators,
)
...
accumulators is a fragment (i.e. lives in RMEM) and initialised as follows:
thr_mma = tiled_mma.get_slice(warp_group_thread_layout(warp_group_idx))
tCgC = thr_mma.partition_C(gC_mnl)
...
acc_shape = tCgC.shape
accumulators = cute.make_fragment(acc_shape, self.acc_dtype)
it has layout ((2,2,32),1,1):((1,2,4),0,0). These layout describes a Layout of 128 elements where 32 planes are stacked and each plane has a row major layout. We can think of it as a generalised row major format, i.e. we lay out in row major in 2 dimensions four elements and than continue with the next plane in the same way etc.
After mainloop finishes, i.e. we are done with the GEMM we need to efficiently write the result to GMEM. In the example at hand that is done via RMEM -> SMEM -> GMEM.
We now will analyse the epilogue.
copy_atom_r2s = sm90_utils.sm90_get_smem_store_op(
self.c_layout,
elem_ty_d=self.c_dtype,
elem_ty_acc=self.acc_dtype,
)
copy_atom_C = cute.make_copy_atom(
cute.nvgpu.warp.StMatrix8x8x16bOp(
self.c_layout.is_m_major_c(),
4,
),
self.c_dtype,
)
For c_dtype = Float16 copy_atom_r2s will give us
cute.make_copy_atom(
StMatrix8x8x16bOp(is_m_major, 4), elem_ty_d, loc=loc, ip=ip
)
We will use the stmatrix operation. As we can read in the PTX docs it will warp wise collectively store one or more matrices to shared memory. As can be seen in the above code we will store four matrices collectively.
Here is the Layout from the PTX docs.
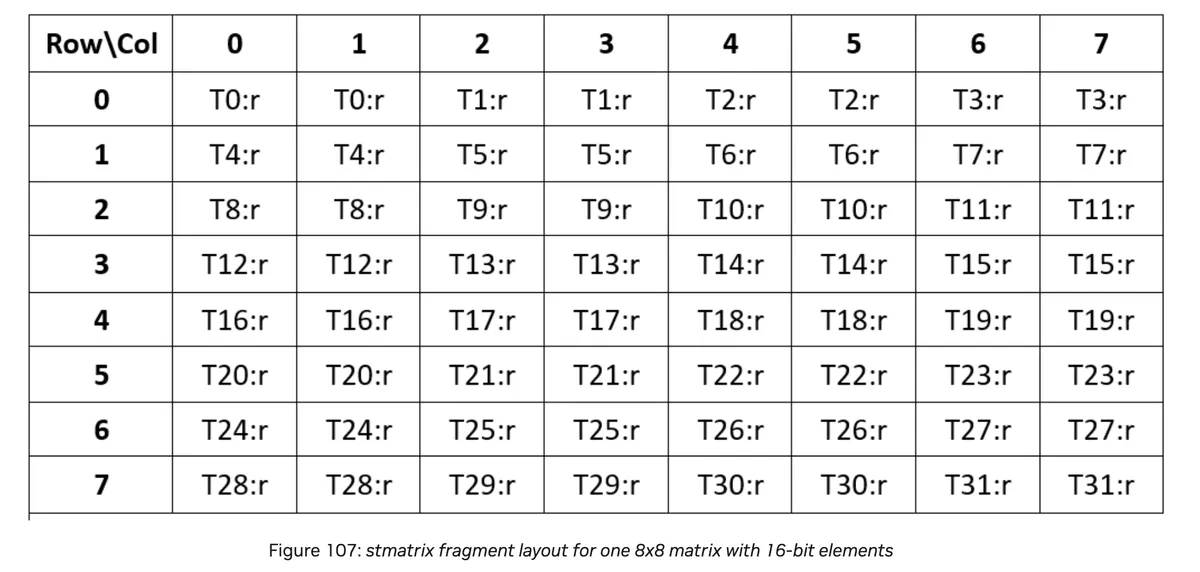
We can furthermore read in the PTX docs that when .num = .x2, the elements of the second matrix are stored from the next source register in each thread as per the layout in above table. Similarly, when .num = .x4, elements of the third and fourth matrices are stored from the subsequent source registers in each thread.
The two Copy Atoms from above look as follows:
Copy Atom
ThrID: 32:1
TV Layout Src: (32,(2,4)):(2,(1,64))
TV Layout Dst: (32,8):(8,1)
Value type: f16
This can be visualised using this script. We see that it is essentially the Layout above transposed and than repeated four times (because we store with .x4).
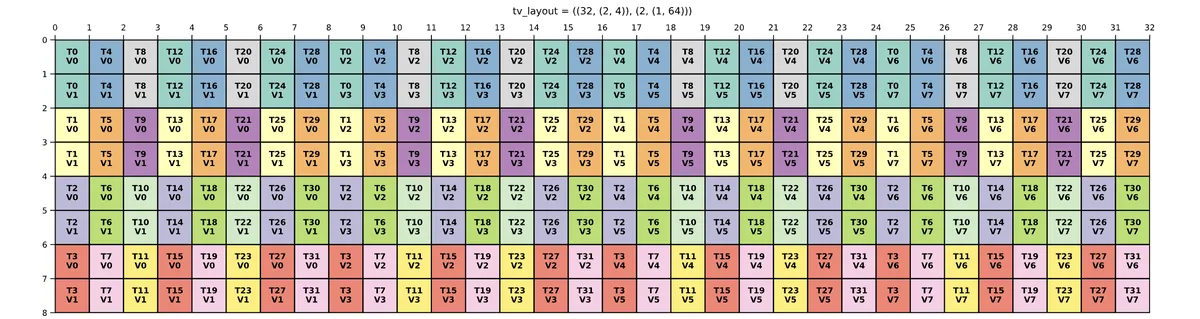
We'll than create
tiled_copy_C_Atom = cute.make_tiled_copy_C_atom(copy_atom_C, tiled_mma)
Which will give us the smallest tiled copy that can retile LayoutC_TV for use with pipelined epilogues with subtiled stores.
And afterwards create a tiled copy out of the copy_atom that matches the Src-Layout of tiled_copy.
tiled_copy_r2s = cute.make_tiled_copy_S(
copy_atom_r2s,
tiled_copy_C_Atom,
)
We'll slice into it, partition (i.e. compose and slice) and retile:
thr_copy_r2s = tiled_copy_r2s.get_slice(tidx)
tRS_sD = thr_copy_r2s.partition_D(sc)
tRS_rAcc = tiled_copy_r2s.retile(accumulators)
tRS_sD = (((2,4),1),1,2,(1,4)):(((1,2),0),0,16,(0,4096))
tRS_rAcc = ((8,16),1,1):((1,8),0,0)
Note that these two obviously have the same size, i.e. 2 * 4 * 1 * 1 * 2 * 1 * 4 = 64 = 8 * 16 * 1 * 1 because we will copy from tRS_rAcc which lives in RMEM to tRS_sD (which we partitioned with partition_D which stands for D(estination)) which lives in SMEM. Note that the last mode (1,4) corresponds to the stages because we will transfer via TMA from SMEM -> GMEM in a staged fashion.
We allocate the registers for d. Note we use partition_S for S(ource). We drop the last mode of the shape because it corresponds to the stage.
# Allocate D registers.
rD_shape = cute.shape(thr_copy_r2s.partition_S(sc))
tRS_rD_layout = cute.make_layout(rD_shape[:3])
tRS_rD = cute.make_fragment_like(tRS_rD_layout, self.acc_dtype)
size_tRS_rD = cute.size(tRS_rD)
tRS_rD = (((2,2,2),1),1,2):(((1,2,4),0),0,8)
We can read that the size is 2 * 2 * 2 * 1 * 1 * 2 = 16 = 64 / 4.
This part of code sets up the TMA
sepi_for_tma_partition = cute.group_modes(sc, 0, 2)
tcgc_for_tma_partition = cute.zipped_divide(gC_mnl, self.epi_tile)
bSG_sD, bSG_gD = cute.nvgpu.cpasync.tma_partition(
tma_atom_c,
0,
cute.make_layout(1),
sepi_for_tma_partition,
tcgc_for_tma_partition,
)
Let us now analyse the epilogue loop
epi_tile_num = cute.size(tcgc_for_tma_partition, mode=[1])
epi_tile_shape = tcgc_for_tma_partition.shape[1]
for epi_idx in cutlass.range(epi_tile_num, unroll=epi_tile_num):
Note that:
gC_mnl = (128,256):(1@1,1@0)
epi_tile = (128,32)
tcgc_for_tma_partition = ((128,32),(1,8)):((1@1,1@0),(0,32@0))
That is we have gC_mnl with shape (bM, bN) and a given epi_tile with shape (bM', bN'). We than use zipped_divide to get a layout that covers (bM, bN) with the given epi_tile and has shape ((bM', bN'), (bM / bM', bN / bN')).
Consequently we get the number of tiles we need to cover by taking the size of the second mode.
We loop over size_tRS_rD. As explained above epi_v indexes into one element of a stage. The stage we are currently in is given by the epi_idx. Note that CuTe algebra makes this complex indexing almost trivial. After having that we store the result (i.e. the accumulators for the current epilogue stage) into tRS_rD_out.
# Copy from accumulators to D registers
for epi_v in cutlass.range_constexpr(size_tRS_rD):
tRS_rD[epi_v] = tRS_rAcc[epi_idx * size_tRS_rD + epi_v]
# Type conversion
tRS_rD_out = cute.make_fragment_like(tRS_rD_layout, self.c_dtype)
acc_vec = tRS_rD.load()
tRS_rD_out.store(acc_vec.to(self.c_dtype))
We use TMA to copy from RMEM to SMEM:
# Copy from D registers to shared memory
epi_buffer = epi_idx % cute.size(tRS_sD, mode=[3])
cute.copy(
tiled_copy_r2s, tRS_rD_out, tRS_sD[(None, None, None, epi_buffer)]
)
cute.arch.fence_proxy(
cute.arch.ProxyKind.async_shared,
space=cute.arch.SharedSpace.shared_cta,
)
# barrier for sync
cute.arch.barrier()
After this we copy to GMEM
# Get the global memory coordinate for the current epi tile.
epi_tile_layout = cute.make_layout(
epi_tile_shape, stride=(epi_tile_shape[1], 1)
)
gmem_coord = epi_tile_layout.get_hier_coord(epi_idx)
# Copy from shared memory to global memory
if warp_idx == 0:
cute.copy(
tma_atom_c,
bSG_sD[(None, epi_buffer)],
bSG_gD[(None, gmem_coord)],
)
cute.arch.cp_async_bulk_commit_group()
cute.arch.cp_async_bulk_wait_group(self.epi_stage - 1, read=True)
cute.arch.barrier()
Note that cute.arch.cp_async_bulk_wait_group(self.epi_stage - 1, read=True) enables overlap of copy from RMEM -> SMEM and SMEM -> GMEM and we leverage the staged approach for the Epilogue here.
Conclusion
I hope this blogpost made Epilogue phase in CuTe kernels more approachable. If you are interested in discussing GPU programming or MLSys in general you can reach out to me via Linkedin.