Backprop through RMSNorm

13 Jul, 2025

$y_{i} = R M S N o r m (x_{i}) = \frac{1}{\sqrt{\sum_{i = 1}^{N} x_{i}^{2} + ϵ}} x_{i} w_{i}$

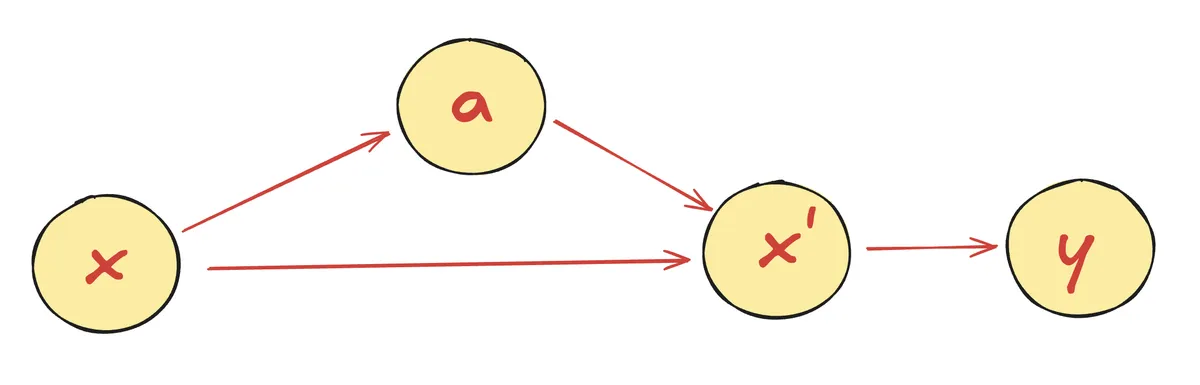
Backprob

$a = \frac{1}{N} \sum_{i = 1}^{N} x_{i}^{2}$ , $x_{i}^{'} = \frac{1}{\sqrt{a + ϵ}} x_{i}$ , $y_{i} = x_{i}^{'} \cdot w_{i}$ , $\partial_{y_{i}} L$ given.

First back propagation:

\partial_{x_{i}^{'}} L = \partial_{y_{i}} L \cdot \partial_{x_{i}^{'}} y_{i} = \partial_{y_{i}} L \cdot w_{i}

Second back propagation: Need to sum over all possible paths from $x^{'}$ to $a$ .

\partial_{a} L = \sum_{j} \partial_{x_{j}^{'}} L \cdot \partial_{a} x_{j}^{'}

\partial_{a} x_{j}^{'} = x_{j} \partial_{a} (a + ϵ)^{- 1 / 2} = - \frac{1}{2} x_{j} (a + ϵ)^{- 3 / 2}

Combine the two expressions gives

\partial_{a} L = - \frac{1}{2 (a + ϵ)^{3 / 2}} \sum_{j} \partial_{y_{j}} L \cdot w_{j} \cdot x_{j}

Third backpropagation: Incoming from two nodes, sum over these:

\partial_{x_{i}} L = \partial_{a} L \cdot \partial_{x_{i}} a + \partial_{x_{i}^{'}} L \cdot \partial_{x_{i}} x_{i}^{'}

First term

\partial_{x_{i}} a = \frac{2}{N} \cdot x_{i}

Second term

\partial_{x_{i}} x_{i}^{'} = \frac{1}{(a + ϵ)^{1 / 2}}

From here it follows

\partial_{x_{i}} L = - \frac{x_{i}}{(a + ϵ)^{3 / 2}} \cdot \frac{1}{N} \sum_{j} \partial_{y_{j}} L \cdot w_{j} \cdot x_{j} + \frac{1}{(a + ϵ)^{1 / 2}} \partial_{y_{i}} L \cdot w_{i} .

Factoring out common terms gives:

\frac{1}{(a + ϵ)^{1 / 2}} (\partial_{y_{i}} L \cdot w_{i} - \frac{x_{i}}{(a + ϵ)^{1 / 2}} \cdot \frac{1}{N} \sum_{j} \partial_{y_{j}} L \cdot w_{j} \cdot \frac{x_{j}}{(a + ϵ)^{1 / 2}}) .

We can simplify further by using definition of $x_{i}^{'}$ :

\frac{1}{(a + ϵ)^{1 / 2}} (\partial_{y_{i}} L \cdot w_{i} - x_{i}^{'} \cdot \frac{1}{N} \sum_{j} \partial_{y_{j}} L \cdot w_{j} \cdot x_{j}^{'}) .

This agrees with reference here

def rmsnorm_bwd_ref(x, w, dout, rstd, eps=1e-6):
    """Reference implementation for RMSNorm backward pass."""
    x_f32 = x.float()
    x_hat = x_f32 * rstd.unsqueeze(1)
    wdy = dout * w
    c1 = (x_hat * wdy).mean(dim=-1, keepdim=True)
    dx = (wdy - x_hat * c1) * rstd.unsqueeze(1)

    # dL/dW
    dw = (dout * x_hat).sum(dim=0)
    return dx.to(x.dtype), dw.to(w.dtype)