Backprob through Layernorm

13 Jul, 2025

Equation for Layernorm:

y_{i} = \frac{x_{i} - m_{i}}{\sqrt{v + ϵ}} w_{i} = x_{i}^{'} w_{i}

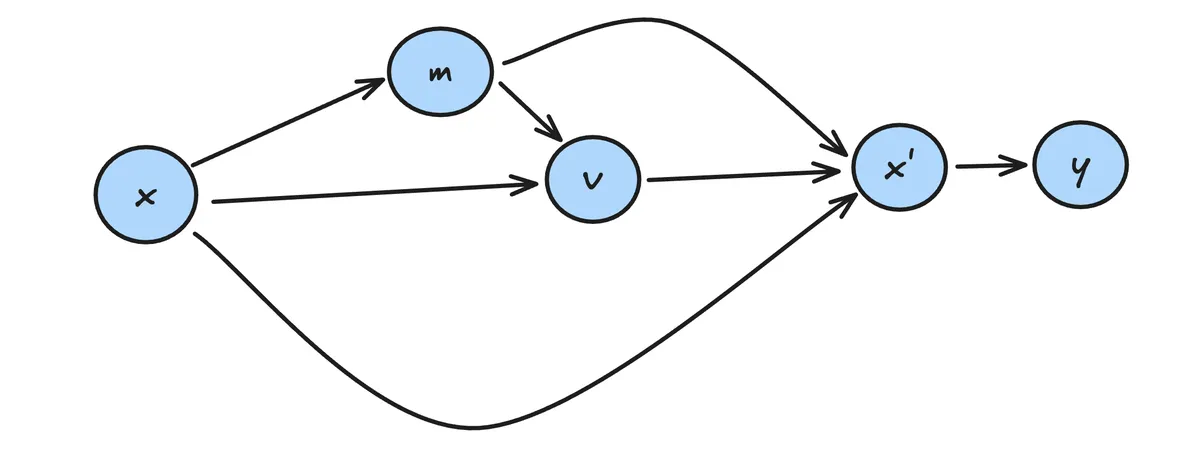
$m = \frac{1}{N} \sum_{i = 1}^{N} x_{i}$ , $v = \frac{1}{N} \sum_{i = 1}^{N} (x - m)^{2}$ , $x_{i}^{'} = \frac{x_{i} - m}{\sqrt{v + ϵ}}$ . As a computational graph: Screenshot 2025-07-13 at 14

$\partial_{y_{i}} L$ given.

\partial_{x_{i}^{'}} L = \partial_{y_{i}} L \cdot w_{i}

Sum over all paths from $x^{'}$ to $v$ .

\partial_{v} L = \sum_{j} \partial_{x_{j}^{'}} L \cdot \partial_{v} x_{j}^{'}

\partial_{v} x_{j}^{'} = (x_{j} - m) \partial_{v} (v + ϵ)^{- 1 / 2} = - \frac{1}{2} (x_{j} - m) (v + ϵ)^{- 3 / 2}

Plugging in:

\partial_{v} L = - \frac{1}{2 (v + ϵ)^{3 / 2}} \sum_{j} \partial_{y_{j}} L \cdot w_{j} \cdot (x_{j} - m)

$m$ has incoming paths from both $x^{'}$ and $v$ . Over the paths from $x^{'}$ we need to sum and sum these with the path from $v$ .

\partial_{m} L = \partial_{v} L \cdot \partial_{m} v + \sum_{j} \partial_{x_{j}^{'}} L \cdot \partial_{m} x_{j}^{'}

\partial_{m} v = \frac{1}{N} \partial_{m} \sum_{j} (x_{j} - m)^{2} = - \frac{2}{N} \sum_{j} (x_{j} - m) = - \frac{2}{N} (\sum_{j} x_{j} - N \cdot \frac{1}{N} \sum_{j} x_{j}) = 0 .

\partial_{m} x_{j}^{'} = \partial_{m} \frac{x - m}{\sqrt{v + ϵ}} = - \frac{1}{\sqrt{v + ϵ}}

Plugging in:

\partial_{m} L = - \frac{1}{(v + ϵ)^{1 / 2}} \sum_{j} \partial_{y_{j}} L \cdot w_{j}

Final backprop: Incoming from $m$ , $v$ and $x^{'}$ .

\partial_{x_{i}} L = \partial_{m} L \cdot \partial_{x_{i}} m + \partial_{v} L \cdot \partial_{x_{i}} v + \partial_{x_{i}^{'}} L \cdot \partial_{x_{i}} x_{i}^{'}

Calculate the terms separately.

First term:

\partial_{x_{i}} m = \partial_{x_{i}} \frac{1}{N} \sum_{j} x_{j} = \frac{1}{N}

\partial_{m} L \cdot \partial_{x_{i}} m = - \frac{1}{(v + ϵ)^{1 / 2}} \frac{1}{N} \sum_{j} \partial_{y_{j}} L \cdot w_{j}

Second term:

\partial_{x_{i}} v = \frac{1}{N} \partial_{x_{i}} \sum_{j} (x_{j} - m)^{2} = \frac{2}{N} (x_{i} - m)

\partial_{v} L \cdot \partial_{x_{i}} v = - \frac{1}{(v + ϵ)^{3 / 2}} \frac{1}{N} (x_{i} - m) \sum_{j} \partial_{y_{j}} L \cdot w_{j} \cdot (x_{j} - m)

We can simplify this using definition of $x^{'}$ .

\partial_{v} L \cdot \partial_{x_{i}} v = - \frac{1}{(v + ϵ)^{1 / 2}} \frac{1}{N} x_{i}^{'} \sum_{j} \partial_{y_{j}} L \cdot w_{j} \cdot x_{j}^{'}

Last term

\partial_{x_{i}} x_{i}^{'} = \partial_{x_{i}} \frac{x_{i} - m}{\sqrt{v + ϵ}} = \frac{1}{\sqrt{v + ϵ}}

\partial_{x_{i}^{'}} L \cdot \partial_{x_{i}} x_{i}^{'} = \partial_{y_{i}} L \cdot w_{i} \cdot \frac{1}{(v + ϵ)^{1 / 2}}

To summarise we have the three terms:

\partial_{m} L \cdot \partial_{x_{i}} m = - \frac{1}{(v + ϵ)^{1 / 2}} \frac{1}{N} \sum_{j} \partial_{y_{j}} L \cdot w_{j}

\partial_{v} L \cdot \partial_{x_{i}} v = - \frac{1}{(v + ϵ)^{1 / 2}} \frac{1}{N} x_{i}^{'} \sum_{j} \partial_{y_{j}} L \cdot w_{j} \cdot x_{j}^{'}

\partial_{x_{i}^{'}} L \cdot \partial_{x_{i}} x_{i}^{'} = \partial_{y_{i}} L \cdot w_{i} \cdot \frac{1}{(v + ϵ)^{1 / 2}}

Now sum these up to obtain final result:

\partial_{x_{i}} L = \frac{1}{(v + ϵ)^{1 / 2}} [\partial_{y_{i}} L \cdot w_{i} - \frac{1}{N} \sum_{j} \partial_{y_{j}} L \cdot w_{j} - x_{i}^{'} \cdot \frac{1}{N} \sum_{j} \partial_{y_{j}} L \cdot w_{j} \cdot x_{j}^{'}]

This is the formula given here.

    @staticmethod
    def backward(dout, cache):
        x, w, mean, rstd = cache
        # recompute the norm (save memory at the cost of compute)
        norm = (x - mean) * rstd
        # gradients for weights, bias
        db = dout.sum((0, 1))
        dw = (dout * norm).sum((0, 1))
        # gradients for input
        dnorm = dout * w
        dx = dnorm - dnorm.mean(-1, keepdim=True) - norm * (dnorm * norm).mean(-1, keepdim=True)
        dx *= rstd
        return dx, dw, db