Applied introduction to Categorical treatment of CuTe

27 Sep, 2025

Introduction

Colfax recently released an excellent paper on the categorical foundations of CuTe. In a previous blog post, I calculated many of the examples from Chapter 2 by hand. In this blog post, I do the same for Chapter 3.

Chapter 3 gives readers a new approach to understanding CuTe Layouts by introducing categories and morphisms that operate on them. It shows how to encode these morphisms into the familiar CuTe Layouts, provides a new visual approach, and offers an alternative perspective on Layouts beyond the traditional treatment. In my opinion it is a very elegant approach that delivers a powerful method of calculations related to CuTe Layouts.

The reasoning behind each example may not be completely straightforward for newcomers, and I hope this small companion guide helps bridge that gap. I focus on building intuition through direct calculation, just as I did for Chapter 2.

For a complete and rigorous treatment, please refer to the original paper.

Learning Notes

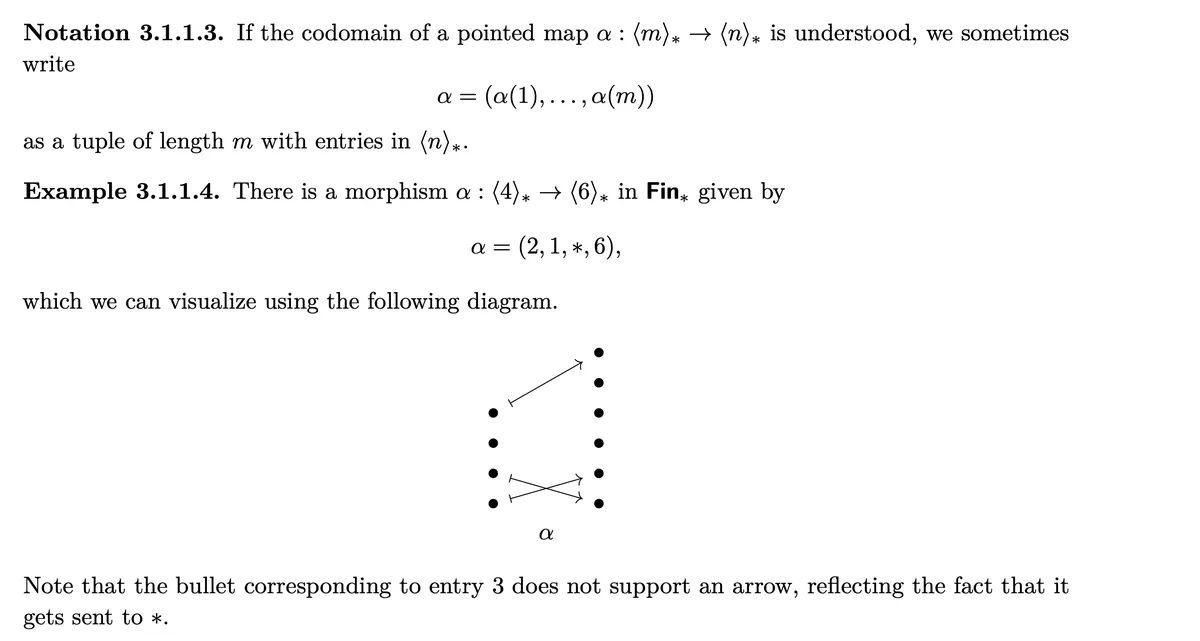
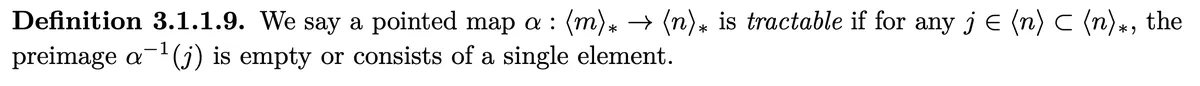
These could be also written down in the following fashion:

• ${\alpha }_1=(1,3)$
• ${\alpha }_2=(*,*,2,4,*)$
• ${\alpha }_3=(3,1,2,5,4)$
• ${\beta }_1=(1,1)$
• ${\beta }_2=(2,*,2,4,*)$
• ${\beta }_3=(2,2,2,5,4)$

Examples:

$S=(3,128,128)$ and $T=(3,2,128,2,128)$, than we can find an $\alpha$ such that $f$ is a tuple morphism by seeing

• $s_1=t_1$
• $s_2=t_3$
• $s_3=t_5$ So $\alpha =(1,3,5)$.

$S=(3,128,128)$ and $T=(128,128)$, than we can find an $\alpha$ such that $f$ is a tuple morphism by seeing

• $s_2=t_1$
• $s_3=t_2$ So $\alpha =(*,1,2)$ or we could also choose $\alpha =(*,2,1)$. We see that we could call $*$ a "Wildcard" if we wanted to emphasise it's meaning.

For example $L=(2,2):(1,2)$ is encoded by $S=(2,2)$, $T=(2,2)$, $\alpha =(1,2)$ because $d_1=1$, $d_2=t_1=2$ where we used that the empty product is $1$. Note we could equivalently choose any number for $t_2$.

Initially visit $(s_0,d_0)=(1,1)$. Start with $d_1$:

• $s_0·d_0=1<d_1=3$, append $(3,2)$ Traverse to $d_2$:
• $s_1·d_1=6<d_2=30$, append $(5,2)$

We have $T=(3,2,5,2)$.

Therefore $S=(2,2)$, $T=(3,2,5,2)$ and $\alpha =(2,4)$ encode the Layout, as depicted in the picture.

Initially visit $(s_0,d_0)=(1,1)$. Start with smallest stride, i.e. $d_2$:

• $s_0{d}_0=d_2$, append $s_2$. Continue with next stride $d_1$:
• $s_2{d}_2=128=d_1$, append $s_1$.

We have $T=(128,128)$ where the first entry corresponds to the second shape, i.e. we have $\alpha =(2,1)$ and than encodes our Layout as depicted above.

Visually that means, that the upper entry has an arrow pointing to it. For all other entries it means that if an entry does not has an arrow to it than the entry is $\ne 1$ and the next entry will have an arrow to it.

Using this intuition the below is clear.

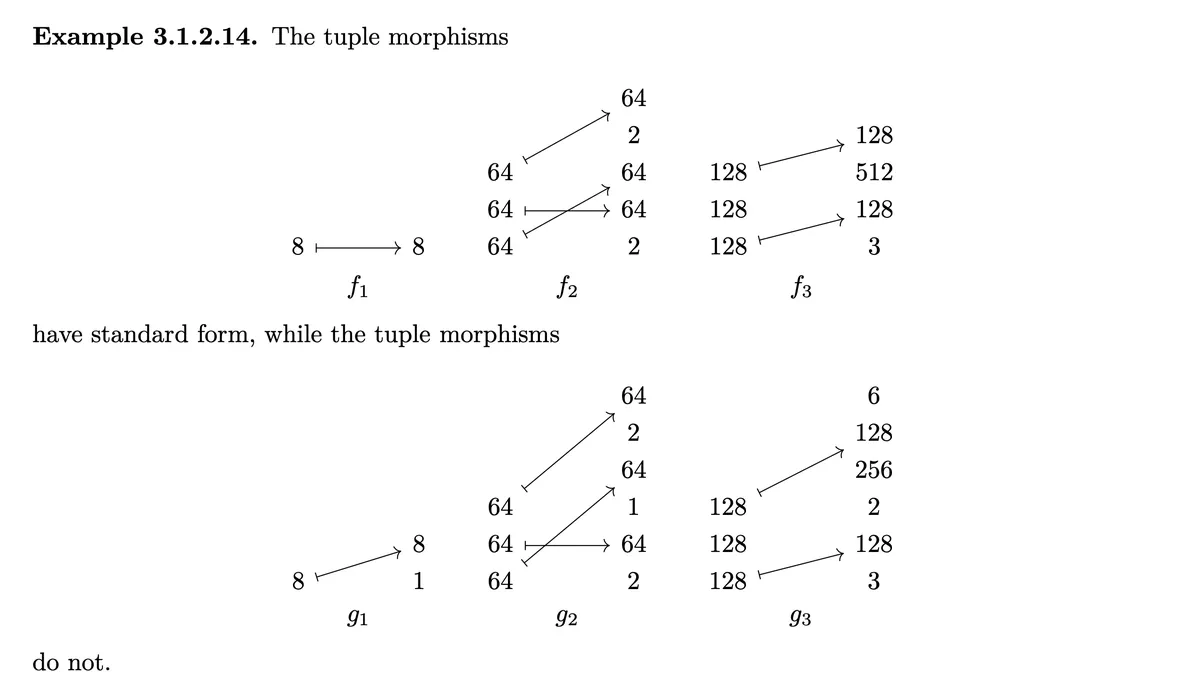
$g_1$ and $g_2$ are not in standard form because they have a one without an arrow to it. $g_3$ is not in standard form because after $2$ which doesn't have an arrow to it there comes $256$ which doesn't have an arrow to it.

Note this is necessary to avoid situations like

$S=(8,1,1)$, $T=(8,1,1)$ where both ${\alpha }_1=(1,2,3)$ as well as ${\alpha }_2=(1,3,2)$ would encode $L=(8,1,1):(1,8,8)$.

That means given a non-degenerate tractable flat layout we can always find a unique encoding for this Layout!

Let's check opposite direction and apply our algorithm from above:

$L=(2,2,2):(1,2,4)$ describes a cube layed out by column first for each plane and each plane is layed out after the previous one.

• $s_0{d}_0=d_1$, so we append $s_1$.
• $s_1{d}_1=d_2$, so we append $s_2$
• $s_2{d}_2=d_3$, so we append $s_3$

Therefore we have $T=(s_1,s_2,s_3)=(2,2,2)$ and $\alpha =(1,2,3)$. This shows very clearly why we call this "identity morphism".

Let's take opposite, i.e. row major

$L=(2,2,2):(4,2,1)$

• $s_0{d}_0=d_3$, so we append $s_3$
• $s_3{d}_3=d_2$, so we append $s_2$
• $s_2{d}_2=d_1$, so we append $s_1$

This means we obtain $T=(s_3,s_2,s_1)$ and $\alpha =(3,2,1)$.

More generally an arbitrary row major Layout with Shape $S=(s_1,...,s_m)$ would give rise to $T=(s_m,...,s_1)$ and $\alpha =(m,m-1,...,2,1)$.

See below for the trivial construction of $g$.

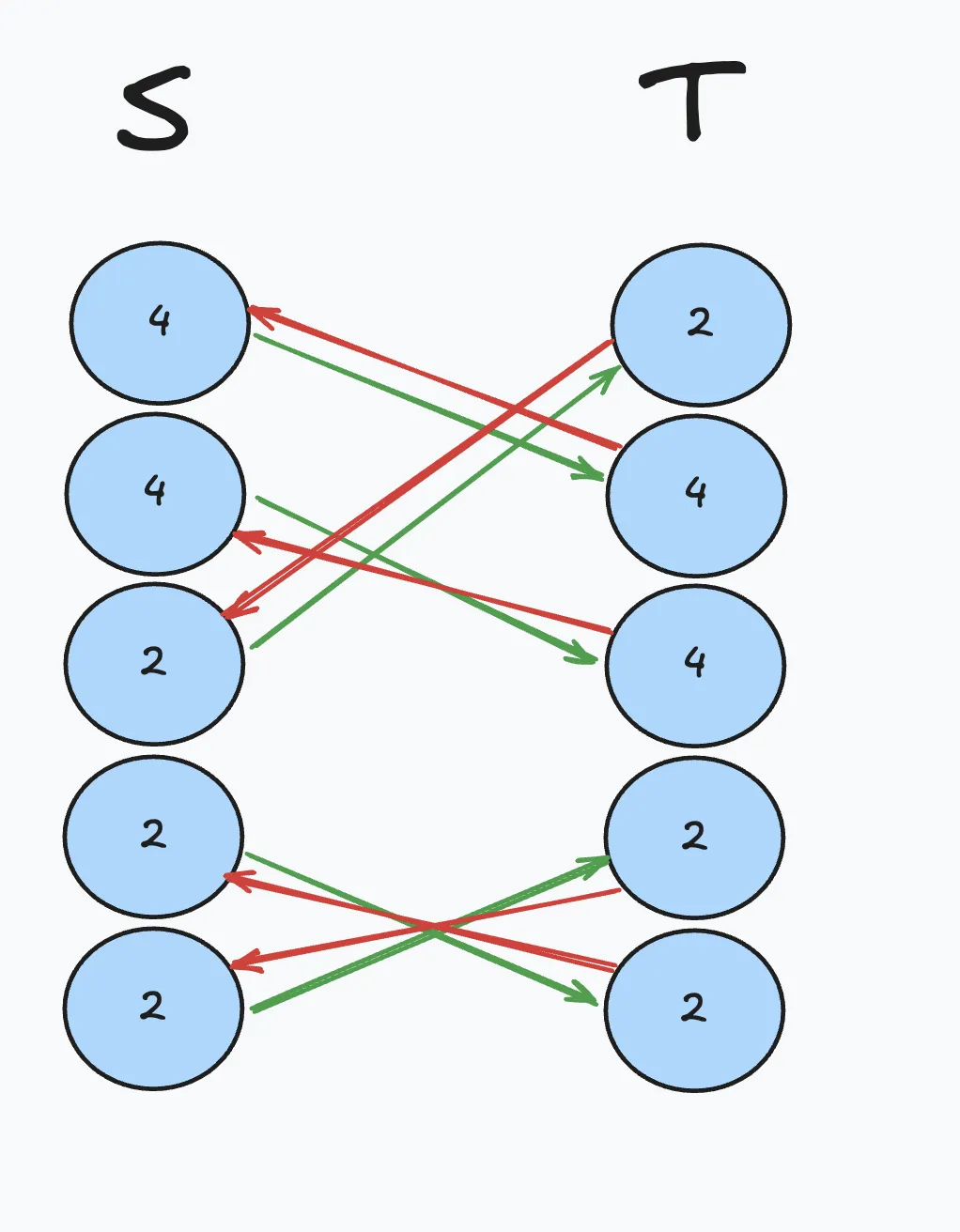
We have $S=(2,2,2,4,4)$, $T=(2,2,4,4,2)$ with isomorphism ${\alpha }_{S\to T}=(2,1,5,3,4)$ leads to $L=(2,2,2,4,4):(2,1,64,4,16)$ and the inverse ${\beta }_{T\to S}=(2,1,4,5,3)$ which leads to $L^{\prime }=(2,2,4,4,2):(2,1,8,32,4)$ .

Let us compose these Layouts in CuTe:

import cutlass.cute as cute

@cute.jit
def inverse():
  L = cute.make_layout(shape=(2,2,2,4,4), stride=(2,1,64,4,16))
  L_ = cute.make_layout(shape=(2,2,4,4,2), stride=(2,1,8,32,4))

  I = cute.composition(L, L_)

  cute.printf(L)
  cute.printf(L_)
  cute.printf(I)

if __name__ == "__main__":
  inverse()

This will output

(2,2,2,4,4):(2,1,64,4,16)
(2,2,4,4,2):(2,1,8,32,4)
(2,2,4,4,2):(1,2,4,16,64) # Stride is (1, 2, 2*2, 2*2*4, 2*2*4*4) = (1,2,4,16,64)

We calculate $L\circ L^{\prime }$ this corresponds to $f\circ g={\mathrm{i}\mathrm{d}}_T$, which corresponds to the column major Layout on $T$. This is exactly what we get in CuTe.

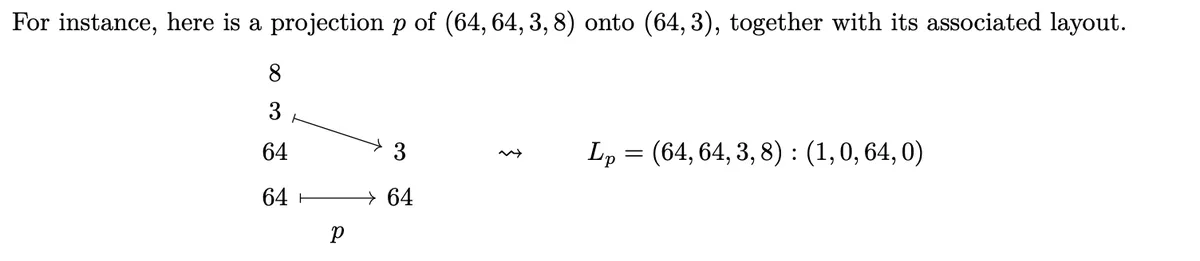
This is called a projection: $S=(8,3,64,64)$, $T=(64,3)$ and $\alpha =(1,*,3,*)$. More general we call a projection if we take some indices $i_1,...,i_R$ and all of these indices have a counterpart where the value in $T$ agrees with the value in $S$. $\alpha$ maps these values and all other values get send to $*$, i.e. the corresponding Layout mode has a stride of $0$.

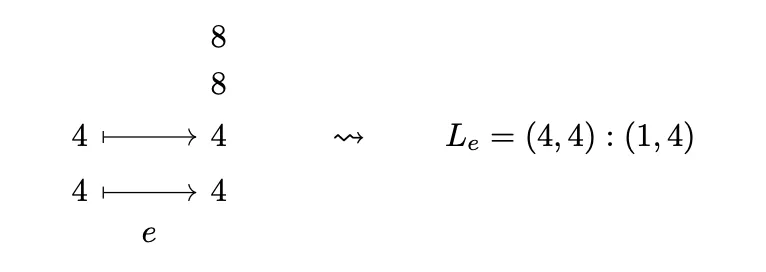
This is an expansion. We call an expansion a morphism from $S=(s_1,...,s_m)$ to $T=(s_1,...,s_m,s_{m+1},...,s_n)$ with $\alpha =(1,...,m)$.

They will have Layouts $L=(s_1,...,s_m):(1,s_1,s_1·s_2,...,s_1·...·s_{m-1})$, i.e. be column major. Note that composition will not do anything, because they are the identity if restricted to their domain in the codomain. Visually this should be also clear because if something "flows in" from the left into the expansion it will just flow in a straight line to the projection domain.

Recall

Lets apply that to the isomorphism $f:(2,2)\to (2,2)$ over $\alpha =(1,2)$.

We have that $Ff(x_1,x_2)=(x_1,x_2)$ and therefore $|f|(x)={\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{x}}_S\circ Ff\circ {\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{x}}_S^{-1}(x)={\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{x}}_S\circ Ff(x\mathrm{mod}2,\lfloor \frac{x}{2}\rfloor \mathrm{mod}2)={\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{x}}_S(x\mathrm{mod}2,\lfloor \frac{x}{2}\rfloor \mathrm{mod}2)=x\mathrm{mod}2+2(\lfloor \frac{x}{2}\rfloor \mathrm{mod}2)$. From here $|f|(0)=0$, $|f|(1)=1$, $|f|(2)=2$, $|f|(3)=3$. The associated Layout is $L=(2,2):(1,2)$ and ${\Phi }_L(x)$ agrees with $|f|(x)$.

We can understand the "sandwiching" of $Ff$ by $\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{x}$ such that we use it to project into higher dimensional space via the inverse, perform our calculation there and project back.

We can therefore calculate the Layout function for arbitrary Layouts by identifying them with their morphism and using the above construction.

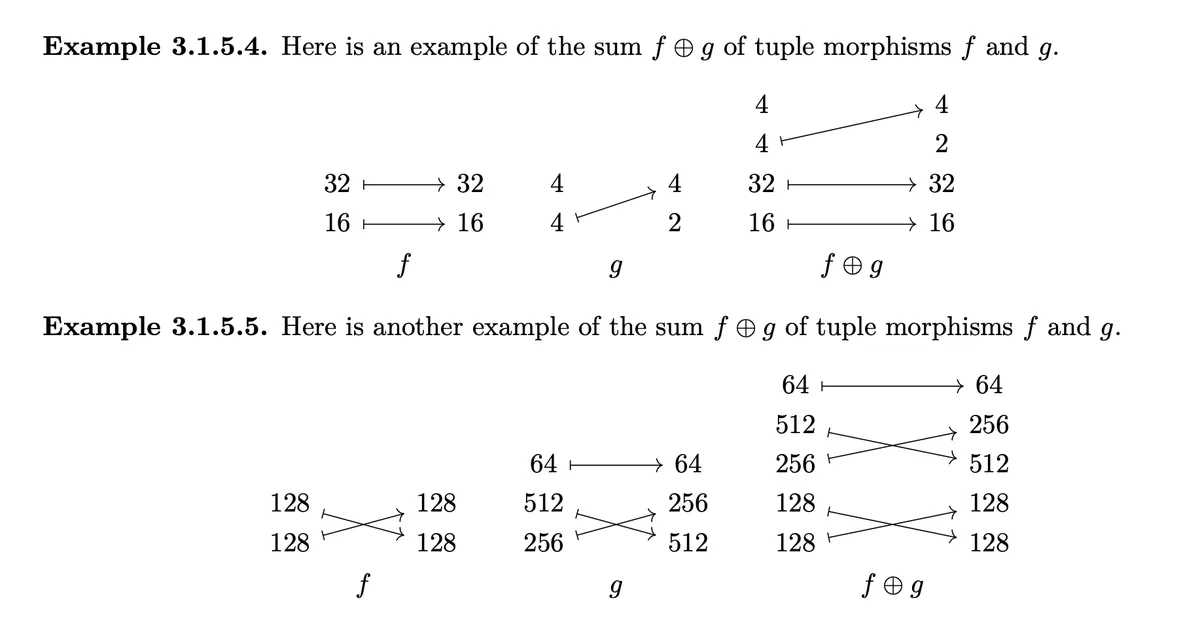
Note that the visuals correspond to the formula: Summing morphisms means extending them by "putting $g$ on top of $f$".

Let us quickly check how the associated Layouts are.

$L_f=(16,32):(1,16)$, $L_g=(4:4):(2,0)$. $f\oplus g$ is the morphism $S=(16,32,4,4)$, $T=(16,32,2,4)$ over $\alpha =(1,2,4,*)$ and the associated Layout is $L_{f\oplus g}=(16,32,4,4):(1,16,1024,0)$. Note that we "extend" the layout into the additional dimensions while scaling the stride appropriately.

Squeezing a Layout just means to to remove redundant modes, i.e. ones with a mode of form $(1,d)$. On morphisms squeezing will remove the ones from $S$, restrict the morphism to the subset of non 1 indices and than factorise, i.e. absorb the ones not in the image of the morphism as described in 3.1.3.10.

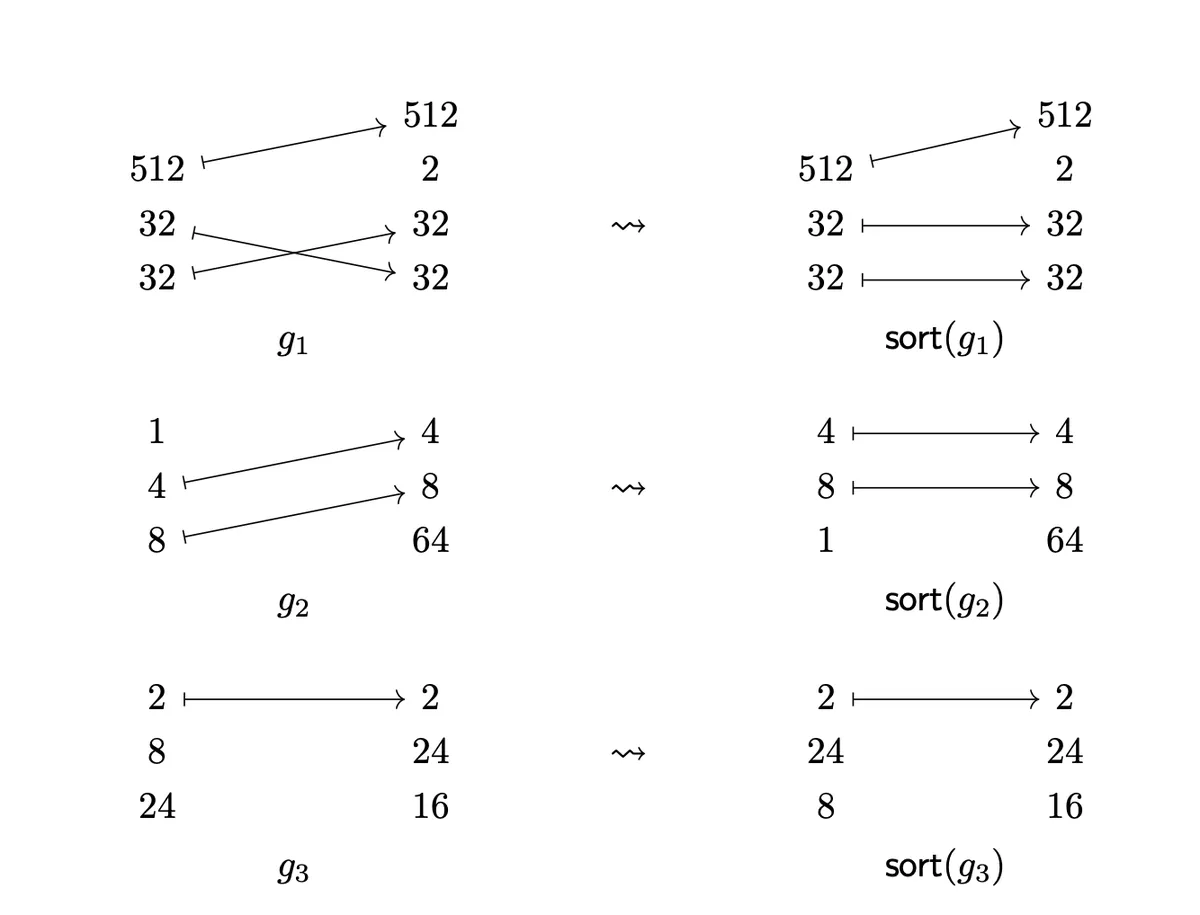
Remember that sorting a Layout will first sort the strides and than within the modes with equal strides by shape. Sorting the morphism means bringing a morphism into arrangement that fulfils above three conditions:

1. If $i$ doesn't have an arrow to the codomain we want it to be before each $j$ that has one.
2. If they both don't have an arrow to the right side we order them by their value $s_i$ and $s_j$
3. We don't want any "crosses" between arrows.

• $g_1$ violates 3).
• $g_2$ violates 1)
• $g_3$ violates 2) In all cases the sorting operation resolves the issues. The Layout of the resulting $\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{t}(g)$ will agree with the sorted Layout corresponding to $g$. Note that sorting a sorted morphism obviously leaves the morphism invariant.

Let us summarise the 4 conditions in 2) in words and give their visual interpretation

1. If $i$ doesn't have an arrow to the right, $i+1$ has one
2. If $i$ has an arrow to the right, than $i+1$ has doesn't have one.
3. $i$ "points" to a higher point in $T$ than $i+1$. (This implies the arrows cross)
4. $i+1$ "points" to a higher point in $T$ than $i$. (This implies the arrows don't cross) Furthermore we have a value larger than one between the two values the two arrows point to. We demand S to be squeezed (i.e. all ones removed) and for each entry except the last one one of the above 4 conditions to be true. Than we say a tuple morphism is coalesced.

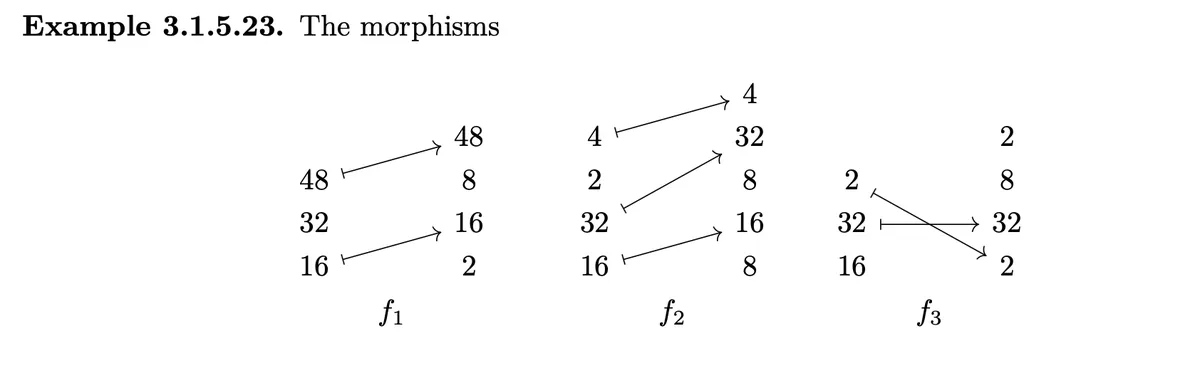
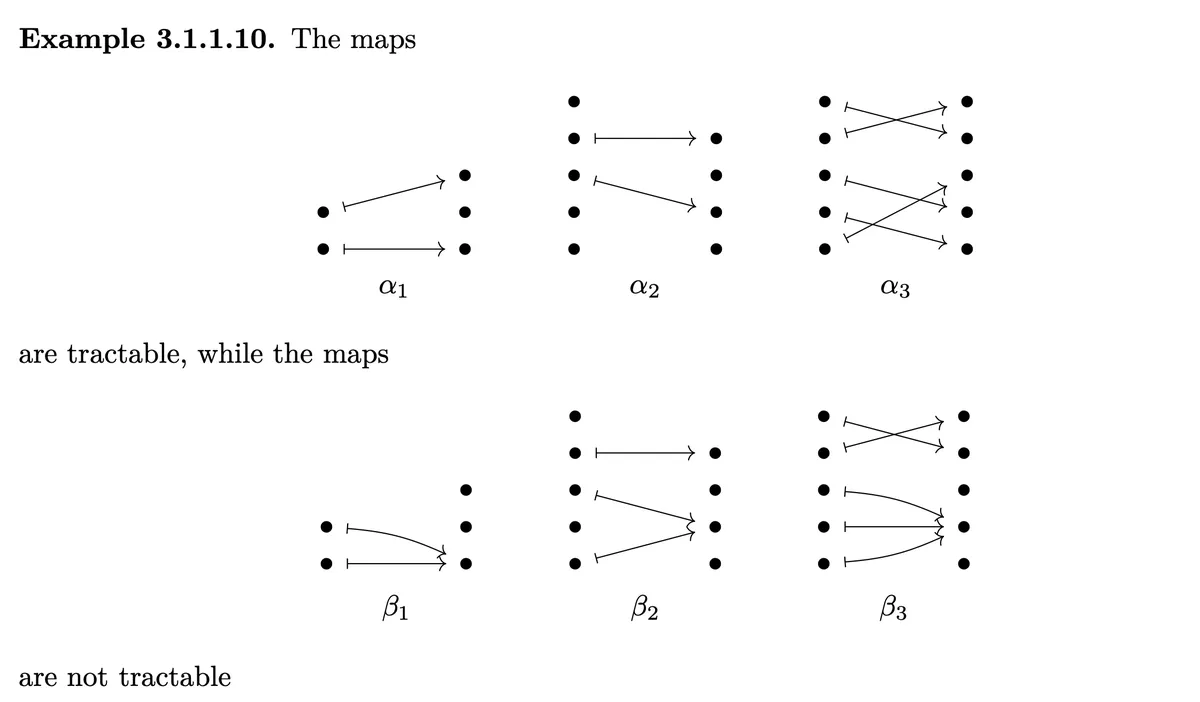
These are examples of coalesced morphisms. Obviously all $S$ are squeezed. To determine if the tuple morphisms are coalesced we need to check above four conditions for each entry except the last:

$f_1$ is coalesced because we have that $1$ has an arrow while $2$ doesn't have one. Furthermore $2$ has not an arrow while $1$ has one.

$f_2$ is coalesced because we have that condition 4) for $1$ and condition 2) for $2$ and condition 1) for $3$.

$f_3$ is coalesced because we have condition 1) for $1$ and condition 3) for $2$.

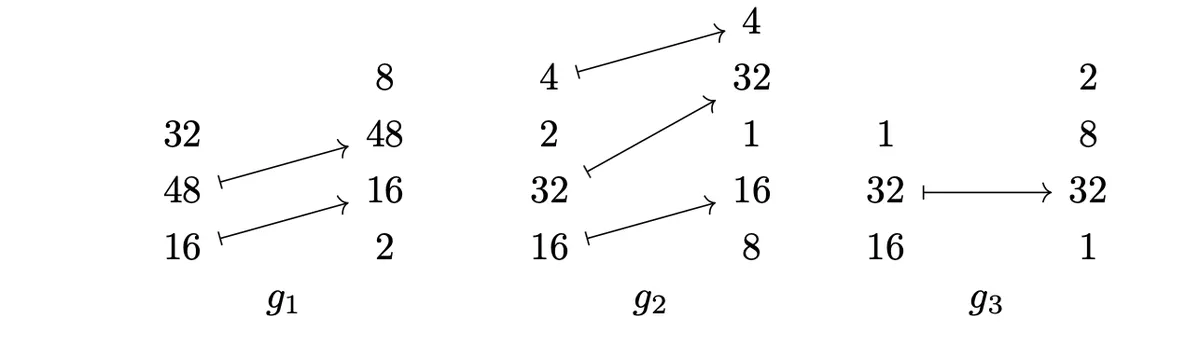
$g_1$ is not coalesced because we have for $1$ that $2$ points to a higher point and there is no value larger than 1 between them.

$g_2$ is not coalesced because $2$ points to a higher point than $1$ and there is only a 1 between them.

$g_3$ is not coalesced because $S$ is unsqueezed.

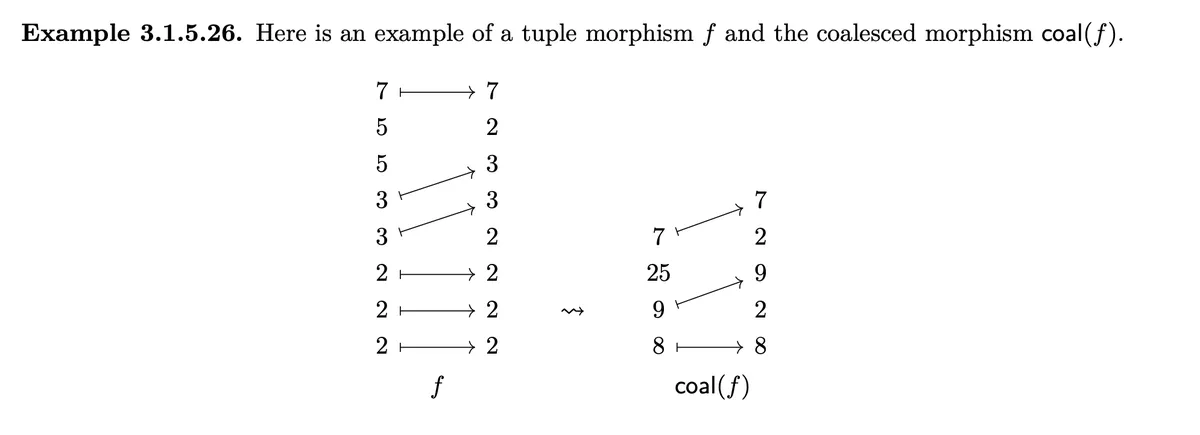
We coalesce $f$ as follows.

• The three 2s "down" violate 4). We multiply them together on left and right and replace the three arrows by one.
• The same is done for the two threes above.
• The two fives violate the condition that on a value without arrow there should follow one with arrow, we multiply them together.

We coalesce $f$ as follows:

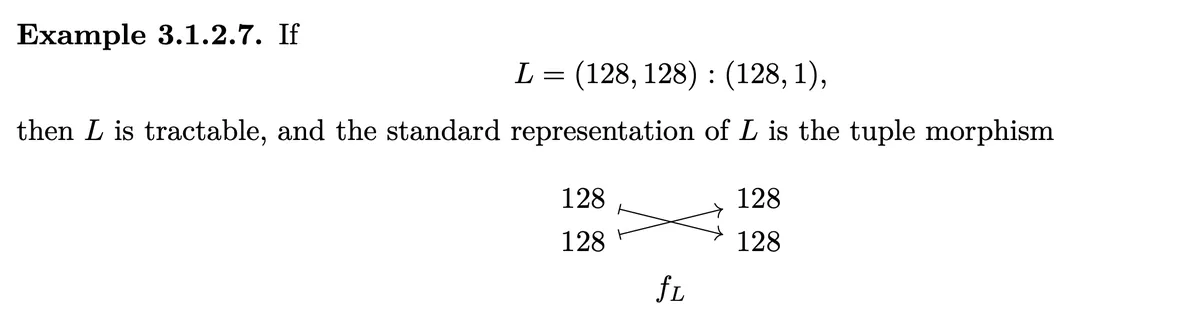
• We first squeeze $S$, i.e. remove all ones from it
• Than 128 and 256 have both an arrow and the mapped values are not separated by value larger than 1. We reduce this by multiplying the corresponding values left and right.

Let's connect it to traditional Layout operation

• $L=(1,8,1,128,256):(0,1,0,8192,1048576)$
• $\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L)=(8,128,256):(1,8192,1048576)$
• Than we perform coalesce, i.e. if $s_i,s_{i+1}:d_i,s_i{d}_i$ than we replace it by $s_i{s}_i+1:d_i$.
• We see that $s_1{d}_1=d_2$ so we reduce $\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}(\mathrm{s}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{z}\mathrm{e}(L))=(8,32768):(1,8192)$. Note that this is precisely the encoding of the morphism above!

Let $f,g,h$ lie over $\alpha ,\beta ,\gamma$. We see $\alpha =(2,4),\beta =(3,1),\gamma =(2,3)$. We see that $\alpha$ is disjoint with $\beta$ but not with $\gamma$. Also $\beta$ is not disjoint with $\gamma$.

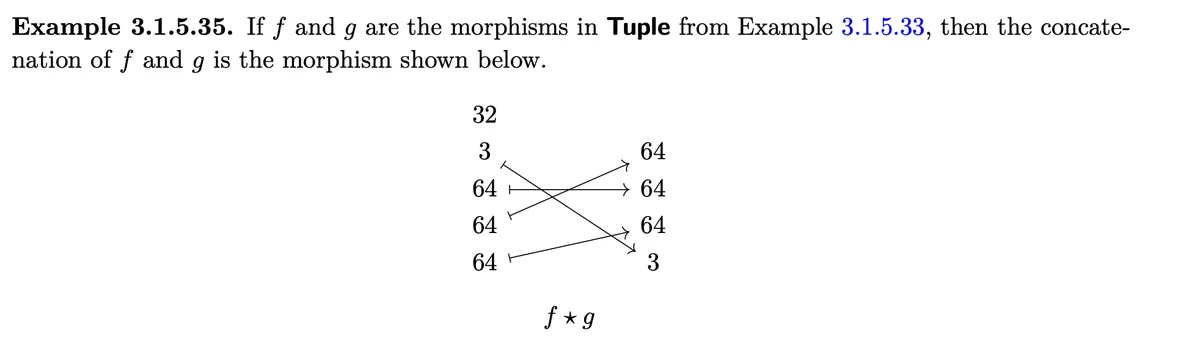
This is the concatenation of the two morphisms. Obviously its tractable, because the images are disjoint (as we see visually as well).

If two morphisms have disjoint image and the concatenation of the two leads to an isomorphism than we say that $g$ is complement of $f$. Note for the above picture that is the case because the concat is obviously bijective and we can therefore construct an inverse to it as done above.

The Layouts associated to $f$ and $g$ are $L_f=(32,32):(10,320)$ and $L_g=(16,10):(10240,1)$, furthermore we have $\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(T)=10·32·32·16=163840$.

Let's calculate the $\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(L_f)$ complement to $L_f$.

• $C=(10,1,16):(1,320,10240)$
• ${\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}}^{♭}(C)=(10,16):(1,10240)$

Note that up to sorting that agrees with $L_g$ from above which is a $\mathrm{s}\mathrm{i}\mathrm{z}\mathrm{e}(T)$ complement of $L_f$. Note that this is given in 3.1.5.48.

Let's understand above example:

$f:(256,512)\to (10,256,512,512)$ with $\alpha =(2,3)$. So we have $(j_1,j_2)=(1,4)$. So we have that $f^c$ is defined from $S=(t_{j_1},t_{j_2})=(10,512)$ to $(10,256,512,512)$ over $\beta =(1,4)$. This is also what we can see in the picture.

$g:(5,5)\to (2,2,5,5)$, $f:(2,2,5,5)\to (2,2,5,5)$.

• $g^c=(2,2)\to (2,2)$
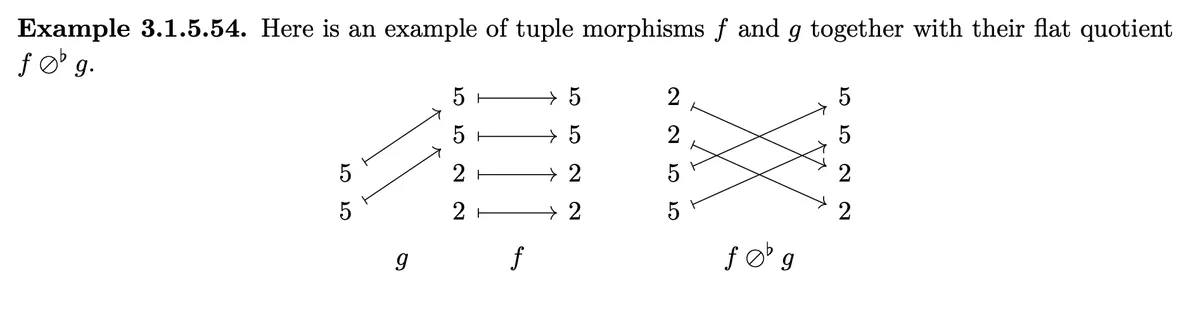
• $g\star g^c:(2,2,5,5)\to (2,2,5,5)$ over $\alpha =(3,4,1,2)$
• Composed with $f$ this will not change because $f$ is the identity.

Here we have $g:(16,16)\to (16,16)$ over $\alpha =(1,2)$ and $f:(8,8)\to (8,8,16,16)$ over $\beta =(1,2)$. Also we have $f^c:(16,16)\to (8,8,16,16)$ over $\gamma =(3,4)$. Let us use that to calculate the flat product. Let us do it visually.

This picture visualises $f^c\circ g$

If we than perform coalesce with $f$ we will obtain the picture shown in above figure.

Lets understand the examples:

1. $S=(64,(8,8))$, $T=(64,8,8)$, $S^{♭}=(64,8,8)$, $T^{♭}=T$, $\alpha =(1,2,3)$.
   • ${\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_1(S)=64={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_{\alpha (1)}(T)={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_1(T)$
   • ${\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_2(S)=8={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_{\alpha (2)}(T)={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_2(T)$
   • ${\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_3(S)=8={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_{\alpha (3)}(T)={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_3(T)$
2. $S=((2,2),2)$, $T=(10,2,2,(3,2,3))$, $S^{♭}=(2,2,2)$, $T^{♭}=(10,2,2,3,2,3)$, $\alpha =(*,5,2)$.
   • ${\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_2(S)=2={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_{\alpha (2)}(T)={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_5(T)$
   • ${\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_3(S)=8={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_{\alpha (3)}(T)={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_2(T)$
3. $S=64$, $T=((64,64),512)$, $S^{♭}=(64)$, $T^{♭}=(64,64,512)$, $\alpha =(2)$.
   • ${\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_1(S)=64={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_{\alpha (1)}(T)={\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{y}}_2(T)$

Let us derive by hand:

$((8,8),(4,4))\to (8,4,4,8)$ over $\alpha =(1,4,3,2)$:

• $P=((*,*),(*,*))$
• $d_1=1$ (empty Product)
• $d_2=8·4·4=128$
• $d_3=8·4=32$
• $d_4=8$
• Equip $\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{e}$ with $P$ gives $\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{e}(L_f)=((1,128),(32,8))$
• Combining with $\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}$ gives $L_f=((8,8),(4,4)):((1,128),(32,8))$

$(128,(4,4,2))\to ((4,4),128)$ over $(3,1,2,*)$

• $P=(*,(*,*,*))$
• $d_1=4·4$
• $d_2=1$, empty product
• $d_3=4$
• $d_4=0$ because $\alpha (4)=*$
• Equip $\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{e}$ with $P$ gives $\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{e}(L_g)=(16,(1,4,0))$
• Combining with $\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}$ gives $L_g=(128,(4,4,2)):(16,(1,4,0))$

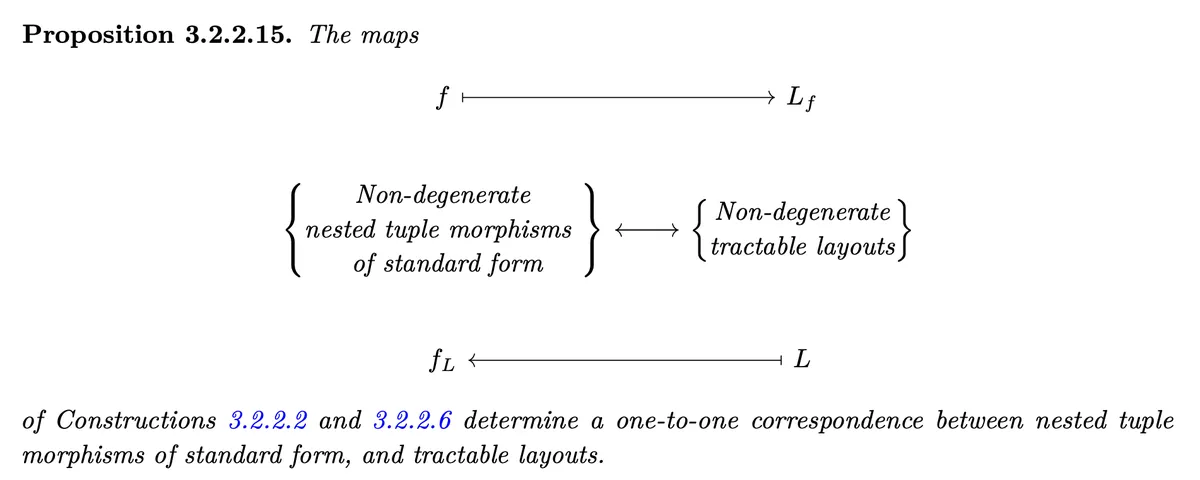
Definition of standard form is similar to above, see 3.2.2.10.

Note that concatenation works such that we define two nested tuples to be in concatenation if the corresponding flattening of nested tuples is in concatenation.

We may note that above we have very clearly for $f^{♭}:(3,512,512)\to (2,512,2,512)$ over $(*,2,4)$ and $g^{♭}:(2,2)\to (2,512,2,512)$ over $(1,3)$ that their concatenation is simply $f^{♭}\star g^{♭}=(3,512,512,2,2)\to (2,512,2,512)$ over $\gamma =(*,2,4,1,3)$. Than using that concat is map from $(S,U)\to T$ as given in 3.2.6.4 will tell us with which profile, i.e. $(P_S,P_U)$, to equip the above flat Layout and we obtain above result. Note that $P_S=(*,(*,*))$ and $P_U=(*,*)$.

Let us calculate above example.

We have that $m=3$, so $\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}(f)={\mathrm{c}\mathrm{o}\mathrm{a}\mathrm{l}}^{♭}(f^{♭})$.

• $f^{♭}=(2,2,3,3,5,5)\to (5,5,3,3,2,2)$ over $\alpha =(5,6,3,4,1,2)$.

Before we continue let's remember:

Let us summarise the 4 conditions in 2) in words and give their visual interpretation

1. If $i$ doesn't have an arrow to the right, $i+1$ has one
2. If $i$ has an arrow to the right, than $i+1$ has doesn't have one.
3. $i$ "points" to a higher point in $T$ than $i+1$. (This implies the arrows cross)
4. $i+1$ "points" to a higher point in $T$ than $i$. (This implies the arrows don't cross) Furthermore we have a value larger than one between the two values the two arrows point to. We demand S to be squeezed (i.e. all ones removed) and for each entry except the last one one of the above 4 conditions to be true. Than we say a tuple morphism is coalesced.

Let us draw picture of $f^{♭}$.

Note that if we reduce the adjacent nodes into one by multiplying (because they violate 4) from above) we will obtain the following picture

Check for the first entry that it obeys rule 3) from above. Check for second entry that it obeys 3) as well. Therefore the morphism is coalesced. It is given by $(4,9,25)\to (25,9,4)$ over $(3,2,1)$.

Let us verify:

• $f^{♭}=(2,2,5,5)\to (2,5,7,2,5,7)$ over $(1,4,2,5)$. Similar to calculation for complement above we have $(j_1,j_2)=(3,6)$ and therefore $(f^{♭}{)}^c:(7,7)\to (2,5,7,2,5,7)$ over $(3,6)$.
• We perform "unflattening" by equipping $T$ with appropriate profile and obtain $f^c:(7,7)\to ((2,5,7),(2,5,7))$ like shown above.

We have obviously that the $\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{o}\mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}(g)$ is $\mathrm{d}\mathrm{o}\mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}(f)$. We have that $g^c:2\to ((2,2),2)$ over $(2)$. Therefore $(g,g^c)=((2,2),2)\to ((2,2),2)$ over $(1,3,2)$. We than compose $\alpha =(2,4,*)$ with $\beta =(1,3,2)$ and this gives $\gamma =\alpha \circ \beta$. Lets determine $\gamma$ by simply substituting the possible values.

• $\gamma (1)=\alpha (\beta (1))=\alpha (1)=2$
• $\gamma (2)=\alpha (\beta (2))=\alpha (3)=*$
• $\gamma (3)=\alpha (\beta (3))=\alpha (2)=4$ Therefore we have that $((2,2),2)\to ((4,2),(4,2))$ over $(2,*,4)$ is the logical product as indicated in the picture.

Conclusion

I hope this paper makes the new calculation mechanism by Colfax more accessible. Please refer to their original Paper and consider starring the accompanying repo on Github. I am happy to connect on Linkedin to exchange ideas.