A short note on Tensorcores and Inline PTX Assembly
Tensorcores are dedicated units on the GPU to perform matrix multiplication.
To leverage their full potential we need to write Inline PTX Assembly.
This short note aims to demystify programming tensor cores by leveraging PTX instructions.
MMA
From the PTX doc we can find:
The matrix multiply and accumulate operation has the following form:
D = A * B + C
where D and C are called accumulators and may refer to the same matrix.
There are two kinds of operations to perform warp level MMA operations:
wmma and mma.
In this blog we will focus on mma instructions due to their higher flexibility. Note that for highest performance on Hopper you should use wgmma instruction.
Half precision instructions for mma have the following form:
mma.sync.aligned.m8n8k4.alayout.blayout.dtype.f16.f16.ctype d, a, b, c;
mma.sync.aligned.m16n8k8.row.col.dtype.f16.f16.ctype d, a, b, c;
mma.sync.aligned.m16n8k16.row.col.dtype.f16.f16.ctype d, a, b, c;
.alayout = {.row, .col};
.blayout = {.row, .col};
.ctype = {.f16, .f32};
.dtype = {.f16, .f32};
Alternate floating point instructions for mma have the following form:
mma.sync.aligned.m16n8k4.row.col.f32.tf32.tf32.f32 d, a, b, c;
mma.sync.aligned.m16n8k8.row.col.f32.atype.btype.f32 d, a, b, c;
mma.sync.aligned.m16n8k16.row.col.f32.bf16.bf16.f32 d, a, b, c;
mma.sync.aligned.shape.row.col.dtype.f8type.f8type.ctype d, a, b, c;
mma.sync.aligned.m16n8k32.row.col.kind.dtype.f8f6f4type.f8f6f4type.ctype d, a, b, c;
.atype = {.bf16, .tf32};
.btype = {.bf16, .tf32};
.f8type = {.e4m3, .e5m2};
.f8f6f4type = {.e4m3, .e5m2, .e3m2, .e2m3, .e2m1};
.ctype = {.f16, .f32};
.dtype = {.f16, .f32};
.shape = {.m16n8k16, .m16n8k32};
.kind = {.kind::f8f6f4};
A skeleton for mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32 can be found in the PTX docs:
mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
Below we can see the layout for the accumulator matrix
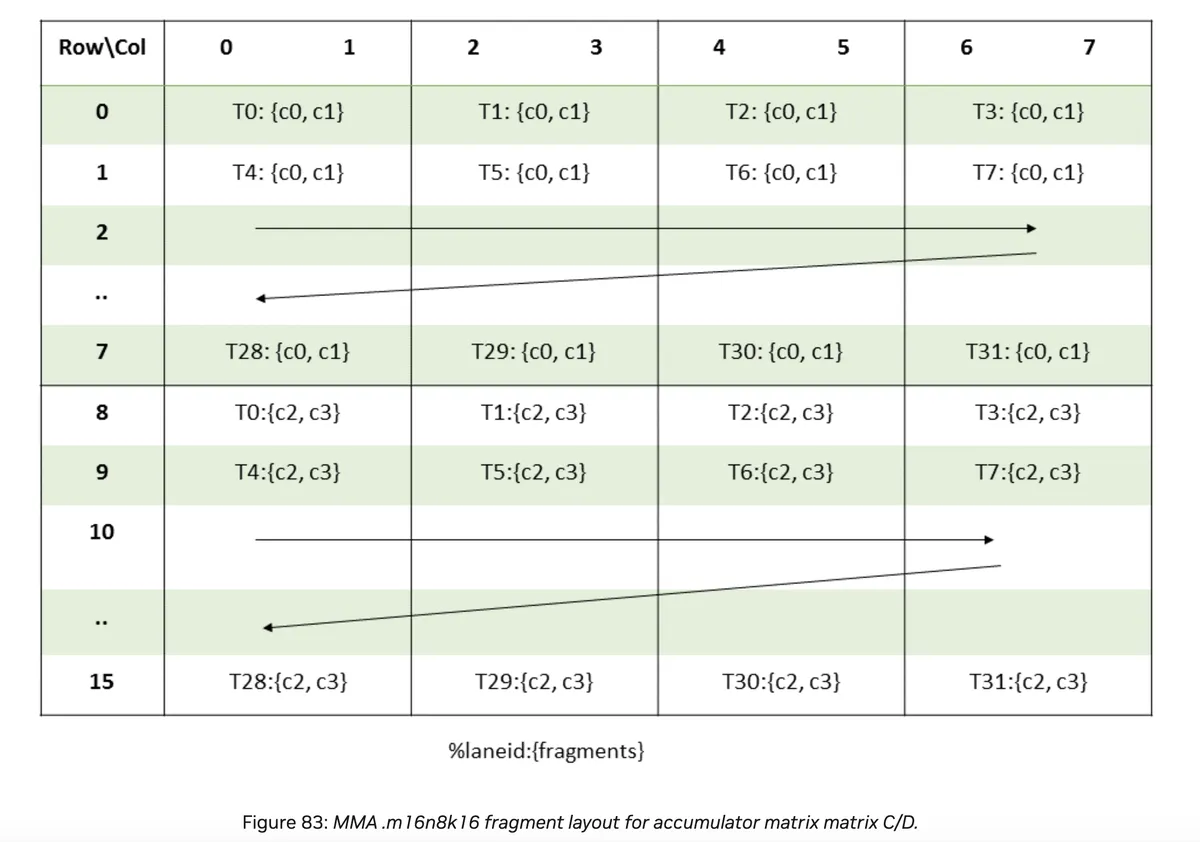
Each thread handles 4 elements c0, c1, c2, c3.
The distance between c1 and c2 is 8 * 8 elements. c0 and c1 together are 8 bytes = 2 * sizeof(float)
Code example taken from stackoverflow.
#include <mma.h>
#include <cuda_fp16.h>
#include <iostream>
#include <stdio.h>
__global__ void mma_fp16_acc_fp32(float *out) {
float c[4] = {0., 0., 0., 0.};
float d[4] = {0., 0., 0., 0.};
half a[8] = {1., 1., 1., 1., 1., 1., 1., 1.};
half b[4] = {1., 1., 1., 1.};
unsigned const *rA = reinterpret_cast<unsigned const *>(&a);
unsigned const *rB = reinterpret_cast<unsigned const *>(&b);
float const *rC = reinterpret_cast<float const *>(&c);
float *rD = reinterpret_cast<float *>(&d);
asm("mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32 "
"{%0,%1,%2,%3}, {%4,%5,%6,%7}, {%8,%9}, {%10,%11,%12,%13};\n"
: "=f"(rD[0]), "=f"(rD[1]), "=f"(rD[2]), "=f"(rD[3])
: "r"(rA[0]), "r"(rA[1]), "r"(rA[2]), "r"(rA[3]), "r"(rB[0]), "r"(rB[1]),
"f"(rC[0]), "f"(rC[1]), "f"(rC[2]), "f"(rC[3]));
memcpy(out + threadIdx.x * 2, rD, 8);
memcpy(out + 8 * 8 + threadIdx.x * 2, rD + 2, 8);
}
int main() {
std::cout << "mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32" << std::endl;
float *h_C = (float *)malloc(16 * 8 * sizeof(float));
float *d_C;
cudaMalloc(&d_C, 16 * 8 * sizeof(float));
mma_fp16_acc_fp32<<<1, 32>>>(d_C);
cudaDeviceSynchronize();
cudaMemcpy(h_C, d_C, 16 * 8 * sizeof(float), cudaMemcpyDeviceToHost);
for (int i = 0; i < 16; i++) {
for (int j = 0; j < 8; j++) std::cout << h_C[i * 8 + j] << " ";
std::cout << std::endl;
}
}
We will now step by step analyse the code:
float c[4] = {0., 0., 0., 0.};
float d[4] = {0., 0., 0., 0.};
half a[8] = {1., 1., 1., 1., 1., 1., 1., 1.};
half b[4] = {1., 1., 1., 1.};
unsigned const *rA = reinterpret_cast<unsigned const *>(&a);
unsigned const *rB = reinterpret_cast<unsigned const *>(&b);
float const *rC = reinterpret_cast<float const *>(&c);
float *rD = reinterpret_cast<float *>(&d);
We perform the operation collectively in a warp.
D = A * B + C where C/D: 16 x 8, A: 16 x 16 and B: 16 x 8.
That means we have 256 / 32 = 8 elements per lane_id for A and 128 / 32 = 4 elements for the others.
The typecasting is necessary to fulfil the constraints on PTX register types:
"h" = .u16 reg
"r" = .u32 reg
"l" = .u64 reg
"q" = .u128 reg
"f" = .f32 reg
"d" = .f64 reg
It means we interpret a as an array with 4 entries where each entry consists of 2 half values. Same for b.
We'll than call
asm("mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32 "
"{%0,%1,%2,%3}, {%4,%5,%6,%7}, {%8,%9}, {%10,%11,%12,%13};\n"
: "=f"(rD[0]), "=f"(rD[1]), "=f"(rD[2]), "=f"(rD[3])
: "r"(rA[0]), "r"(rA[1]), "r"(rA[2]), "r"(rA[3]), "r"(rB[0]), "r"(rB[1]),
"f"(rC[0]), "f"(rC[1]), "f"(rC[2]), "f"(rC[3]));
Afterwards we transfer to the output array with
memcpy(out + threadIdx.x * 2, rD, 8);
memcpy(out + 8 * 8 + threadIdx.x * 2, rD + 2, 8);
This can be understood by looking at the layout above. We write the first 8 bytes (i.e. 2 entries) to the upper part of the layout, than skip 8 * 8 = 64 entries and write the last 8 bytes to the corresponding location at the lower half of the layout.
If we want to choose bfloat16datatype instead for A and B that is as simple as
#define bf16 __nv_bfloat16
#define f2bf16 __float2bfloat16
__global__ void mma_fp16_acc_fp32(float *out) {
float c[4] = {0., 0., 0., 0.};
float d[4] = {0., 0., 0., 0.};
bf16 a[8] = {f2bf16(1.), f2bf16(1.), f2bf16(1.), f2bf16(1.),
f2bf16(1.), f2bf16(1.), f2bf16(1.), f2bf16(1.)};
bf16 b[4] = {f2bf16(1.), f2bf16(1.), f2bf16(1.), f2bf16(1.)};
unsigned const *rA = reinterpret_cast<unsigned const *>(&a);
unsigned const *rB = reinterpret_cast<unsigned const *>(&b);
float const *rC = reinterpret_cast<float const *>(&c);
float *rD = reinterpret_cast<float *>(&d);
asm("mma.sync.aligned.m16n8k16.row.col.f32.bf16.bf16.f32 "
"{%0,%1,%2,%3}, {%4,%5,%6,%7}, {%8,%9}, {%10,%11,%12,%13};\n"
: "=f"(rD[0]), "=f"(rD[1]), "=f"(rD[2]), "=f"(rD[3])
: "r"(rA[0]), "r"(rA[1]), "r"(rA[2]), "r"(rA[3]), "r"(rB[0]), "r"(rB[1]),
"f"(rC[0]), "f"(rC[1]), "f"(rC[2]), "f"(rC[3]));
memcpy(out + threadIdx.x * 2, rD, 8);
memcpy(out + 8 * 8 + threadIdx.x * 2, rD + 2, 8);
}
Very similar we can use float8 input matrices:
#define f8 __nv_fp8_e4m3
__global__ void mma_fp8_acc_fp32(float *out) {
float c[4] = {0., 0., 0., 0.};
float d[4] = {0., 0., 0., 0.};
f8 a[8] = {f8(1.), f8(1.), f8(1.), f8(1.), f8(1.), f8(1.), f8(1.), f8(1.)};
f8 b[4] = {f8(1.), f8(1.), f8(1.), f8(1.)};
unsigned const *rA = reinterpret_cast<unsigned const *>(&a);
unsigned const *rB = reinterpret_cast<unsigned const *>(&b);
float const *rC = reinterpret_cast<float const *>(&c);
float *rD = reinterpret_cast<float *>(&d);
asm("mma.sync.aligned.m16n8k16.row.col.f32.e4m3.e4m3.f32 "
"{%0,%1,%2,%3}, {%4,%5}, {%6}, {%7,%8,%9,%10};\n"
: "=f"(rD[0]), "=f"(rD[1]), "=f"(rD[2]), "=f"(rD[3])
: "r"(rA[0]), "r"(rA[1]), "r"(rB[0]), "f"(rC[0]), "f"(rC[1]), "f"(rC[2]),
"f"(rC[3]));
memcpy(out + threadIdx.x * 2, rD, 8);
memcpy(out + 8 * 8 + threadIdx.x * 2, rD + 2, 8);
}
Note that we need less registers for a and b because sizeof(half)/sizeof(fp8)=2.
Brief analysis of SASS
We can load at SASS code (for example using godbolt) to understand the different SASS instructions used to perform matrix multiplication on tensor cores. The relevant instruction is HMMA which is responsible for the matrix multiply on tensor core.
mma_fp16_acc_fp32(float*):
...
HMMA.16816.F32 R4, R4, R10, RZ
...
mma_bfp16_acc_fp32(float*):
...
HMMA.16816.F32.BF16 R4, R4, R10, RZ
...
mma_fp8_acc_fp32(float*):
...
HMMA.1688.F32 R8, R4, R4, RZ
NOP
HMMA.1688.F32 R4, R4, R4, R8
...
It is interesting to observe that the float8 kernel performs two HMMA.1688.F32 instructions instead of something like HMMA.16816.F32.F8.